FABNet
FABNet: Frequency-Aware Binarized Network for Single Image Super-Resolution
2023 IEEE Transactions on Image Processing
0. 摘要翻译
BNN在实时性和 SISR 方法的性能上取得了标志性成果。现有的方法总是采用 Sign 函数来量化图片特征,但是忽略了图片的空间频率信息。我们认为可以考虑不同的空间频率组件来最小化量化误差。为了实现这个目标,我们为 SISR 提出了频率感知二值网络(FABNet)。首先,我们利用了小波变换把特征分解为低频和高频组件。然后应用“分而治之”策略,使用设计良好的二值网络结构来分别处理他们。此外,我们引入了一个动态二值化过程,包含了在前向传播过程中使用学习阈值进行二值化,在反向传播过程中动态近似,这高效的解决了多样的空间频率信息。相比现有方法,我们的方法在减小量化误差和恢复图像纹理方面是有效的。扩展实验在四个基准数据集上进行,证实了这种方法在峰值信噪比(PSNR)和视觉质量方面均优于现有方法,同时保持了显著降低的计算成本。
1. INTRODUTION
图像超分的轻量化研究方向可以粗糙的分为两个方向:
- 设计更小的网络,以减小网络权重和浮点操作。
group convolution
squeeze operations
finding the best topology - 通过减小权重的位宽或者大小来降低模型内存
pruning
quantization
基于 BNN 的方法有天然的硬件优势:1)内存节省;2)效率更高;3)显著加速。
图像分类任务 BNN 做的比较好是因为,直接学习从输入到输出的(logits)关系。而 SR 任务需要依赖像素值的精度,二值化会给包
含纹理和细节的特征图带来巨大的信息损失。所以目前 SR 领域基于 BNN 的方法和基于浮点网络的方法,还有很大的效果差距。
作者提出了当前 BNN 存在的两个 issues:
- 图像空间维度带来的量化误差被忽视了;高频区域的像素点变化剧烈,二值特征不能反映原始像素的差异。因此使用相同的二值函数处理不同空间频率的信息不能得到最佳的 SR 效果。
- 当前的 SR 方法不修改全精度网络的结构,直接用在 BNN 上并 不好。并且二值化上采样模块带来了极大的效率下降,而保留全精度的上采样层又会给推理过程带来大量的复杂运算。
作者首次提出了考虑图片的空间变化。自然图像有低频和高频分量组成:低频分量反映了平滑的结构;高频分量反映了快速变化的细节。
作者提出了 frequency-aware binarized network(FABNet),实现过程大致如下:
使用离散小波变换(discrete wavelet transform, DWT)来分解全精度特征为低频和高频分量。然后用设计良好的二值网络结构分别处理低高频分量。引入了适应不同空间频率信息的动态二值化处理。通过小波变换(DWT)和逆小波变换(IDWT)实现了无信息损失的下采样和上采样过程。
2. RELATED WORK
现有的基于 BNN 的 SR 方法,主要思想是减少前向传播中的量化误差和避免反向传播中的梯度消失。但是,作者认为仅仅关注减少量化误差和提高梯度传递的方法已经到达了瓶颈。但是从图像空间维度考虑量化误差,仍有研究的空间。
3. MOTIVATION
每个全精度的特征,局部都保留了它的特征表述。对所有位置应用同一个空间共享二值函数显然是不合适的。但是对每个位置学习一个特定的二值函数又不现实。不同频率区间,像素对二值函数的敏感程度不同,高频区间浮点像素变化剧烈(如下图2所示),二值化特征没法反映原始像素间的差异。所以作者选择通过 DWT 将全精度特征分解到高频和低频的区间上分别处理。
4. METHOD
现有的二值 SR 结构可以被分为两种框架:
-
pre-upsampling framework:这种二值网络学习对插值 LR 图像的端到端的映射。
这种超分过程可以表示为: $I_{SR}=\mathcal{I}(\mathcal{D}(\mathcal{S} (I_{LR}^{interpolated})))$ 。 $\mathcal{S}$ 使用全精度卷积层将图像转换为浅层特征;$\mathcal{D}$ 由二值卷积层堆叠而成,主要任务是将浅层特征映射到深层特征;$\mathcal{I}$ 利用全精度网络实现了将深度特征转化为图片。
-
post-upsampling framework:
这种过程可以表述为:$I_{SR}= \mathcal{I}(\mathcal{U}(\mathcal{D}(\mathcal{S}(I_{LR}))))$ 。$\mathcal{U}$ 代表了上采样模块,来提升图像的分辨率。直接二值化上采样模块会导致性能急剧下降,所以以往基于 BNN 的 SR 方法仅仅二值化 $\mathcal{D}$ 部分,但是 $\mathcal{U}$ 部分占了计算量的很大一部分。
4.1 回顾作者提出的 framework
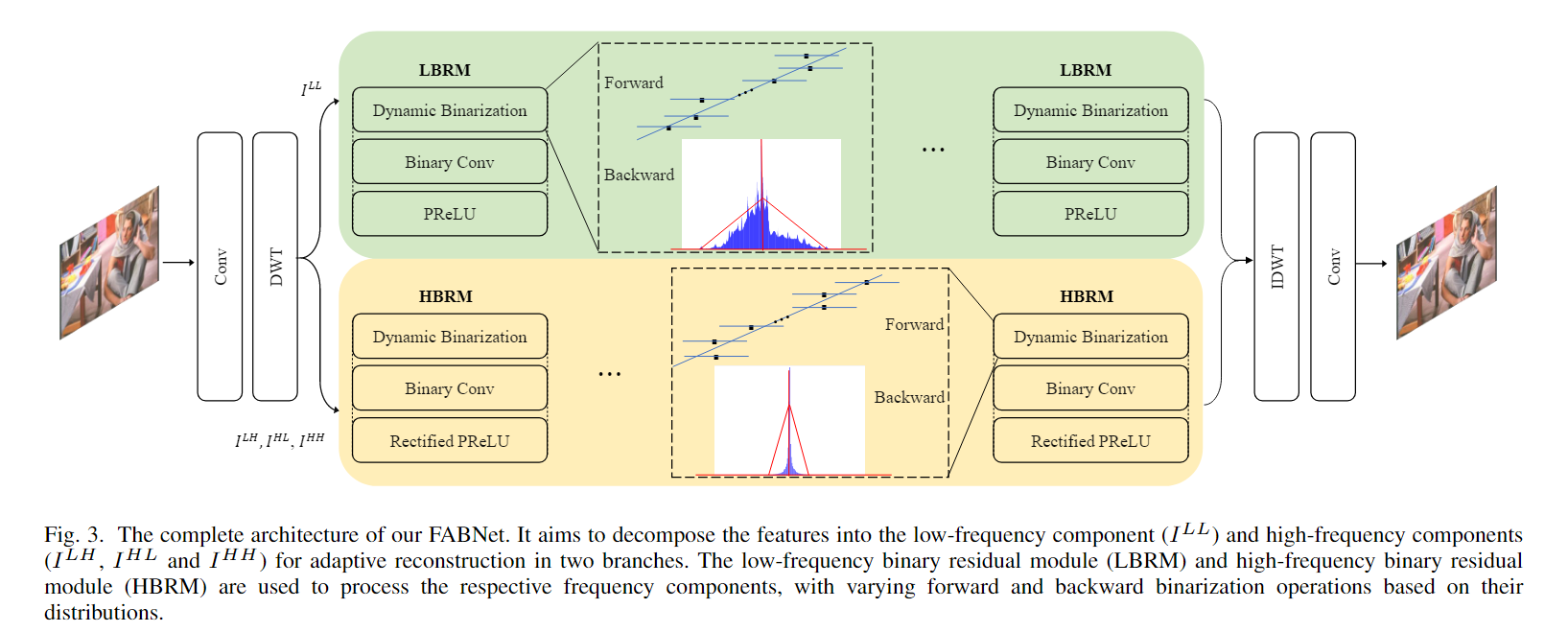
本文的方法,取一张插值的 LR 图像,第一层和最后一层保留全精度网络,其他层进行二值操作。框架实现细节,如下图 Fig.3 所示。
给定一张输入图像 $I_{LR}^{interpolated}$ ,首先使用全精度卷积层提取 low-level 特征:
$$
I^0 = F_{conv}(I_{LR}^{interpolated}) \tag{1}
$$
$F_{conv}$ 代表全精度卷积操作。 $I^0$ 表示提取到的浅层特征。然后将 $I^0$ 分解为1个低频空间组件和3个高频空间组件:
$$
I^{LL},I^{LH},I^{HL},I^{HH}=DWT(I^0) \tag{2}
$$
$I^{LL},I^{LH},I^{HL},I^{HH}$ 分别代表了 $I^0$ 的平均,水平,垂直和对角线组件。DWT 代表离散小波变换操作。之后的推导过程中,对其使用本文提出的“分而治之”的策略。低频部分($I^{LL}$)和高频部分($I^{LH},I^{HL},I^{HH}$)分别由不同的分支处理。每个组件都被输入到针对频率特征设计良好的二值网络架构中。处理过程可以表述为:
$$
I^{LL’}=F_L(I^{LL}) \tag{3}
$$
$$
I^H = Cat(I^{LH},I^{HL},I^{HH}) \tag{4}
$$
$$
I^{H’} = F_H(I^H) \tag{5}
$$
$F_L,F_H$ 表示两种不同的特征映射分支。 $Cat(.)$ 表示通道连接操作。 $I^{LL’}$ 和 $I^{H’}$ 表示不同空间频率的深度特征。$I^{H’}$ 可以被沿着通道维度分开,得到三个特征映射子集 $I^{LH’},I^{HL’},I^{HH’}$ 。
最后,通过逆小波变换(inverse discrete wavelet transformation, IDWT)重建强化后的特征如下:
$$
I^F = IDWT(I^{LL’},I^{LH’},I^{HL’},I^{HH’}) \tag{6}
$$
其中,$I^F$ 表示深度特征,然后利用全精度卷积层处理它
$$
I^{SR} = H_{conv}(I^F)+I^{interpolated}{LR} \tag{7}
$$
$H{conv}$ 表示最后一层,即全精度的卷积层。
然后通过最小化重建的 SR 图像和 GT 之间的逐像素 L1 loss 进行二值 SR 模型的优化。
给定一个训练集 ${I_i^{LR},I_i^{HR}}^N_{i=1}$ ,包含 $N$ 个 LR 输入和其对应的 HR 。loss 定义如下:
$$
L(W) = \frac{1}{N} \sum_{i=1}^N| I_i^{HR} - I_i^{SR} |_1 \tag{8}
$$
$|.|_1$ 表示 L1 正则化,$W$ 表示网络参数。
4.2 分而治之二值残差模块
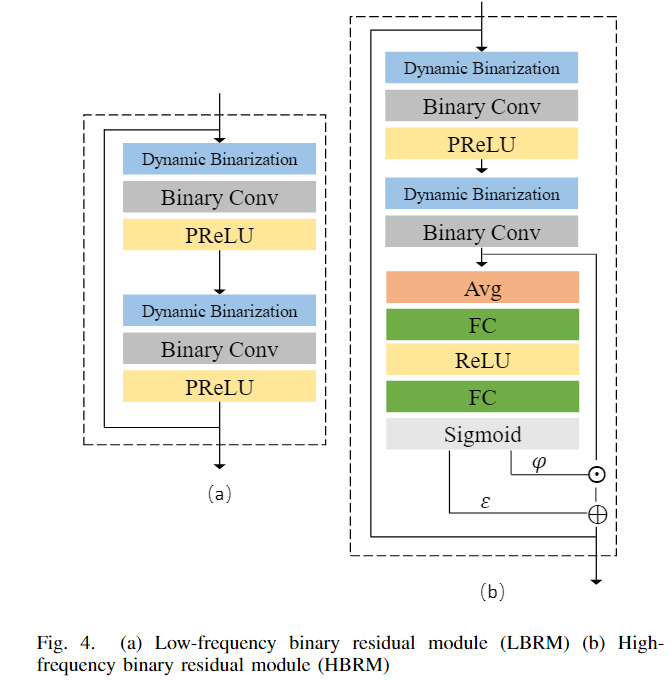
本文的方法中,保留了“分而治之”的策略处理不同频率的信息。低频分支更注重保护低频信息,高频分支更多关注高频信息的复原。如上图 Fig.3 所示,低频分支由多个 low-frequency binary residual modules(LBRM) 组成,高频分支由多个 high-frequency binary residual modules(HBRM) 组成。对于每个二值模块,使用一个基本配置:Binary Activation → Binary Conv → Activation 。
Binary Activation
在前向传播中,大多数现存方法使用 sign 函数将实值变量转化为二值:
$$
x^b = sign(x) =
\begin{cases}+1 &\text{if } x \geqslant 0 \
-1 &\text{otherwise}
\end{cases}
\tag{9}
$$
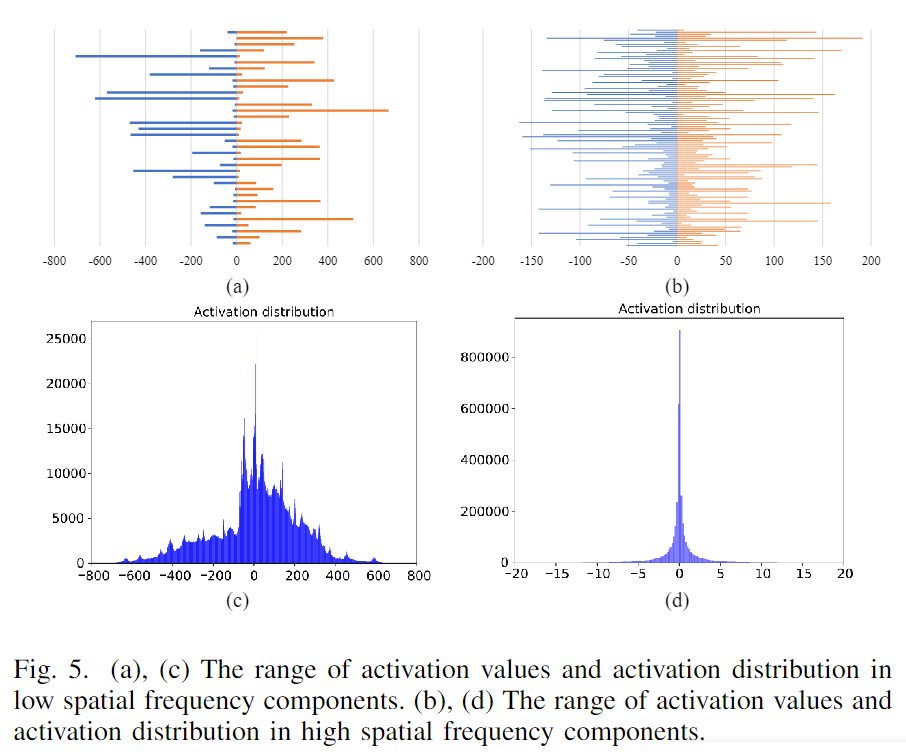
很显然二值表示只与激活的分布相关。在 Fig.5© 和 (d) 中,作者表示了低频和高频空间组件的激活分布。低空间频率组件的激活分布更无序并拥有更宽的范围。
Fig.5(a)©展示了不同通道上激活的数值范围。可以看出不同通道上激活分布的变化很剧烈,如果仅仅以 0 作为分割线显然是粗糙的。
为了使不同的 components 可以用到特定的二值函数,作者引入了一组可学习的阈值来平移激活分布。
$$
x^b = sign(x- \varepsilon) =
\begin{cases}
+1 &\text{if }x \geqslant \varepsilon \
-1 &\text{otherwise}
\end{cases}
\tag{10}
$$
$\varepsilon$ 就是可学习的阈值,对于不同的 channels, layers 和频率分支是不同的。可以通过模型优化得到最佳阈值,从而得到 channels, layers 和频率分支上的最佳二值表示。
Backward Update in Binarization
反向传播过程中,由于 sign 函数不可微,所以其导数近似为 STE:
$$
\frac{\partial sign(x)}{\partial x} =
\begin{cases}
1 &\text{if }|x| \leq 1 \
0 &\text{otherwise}
\end{cases}
\tag{11}
$$
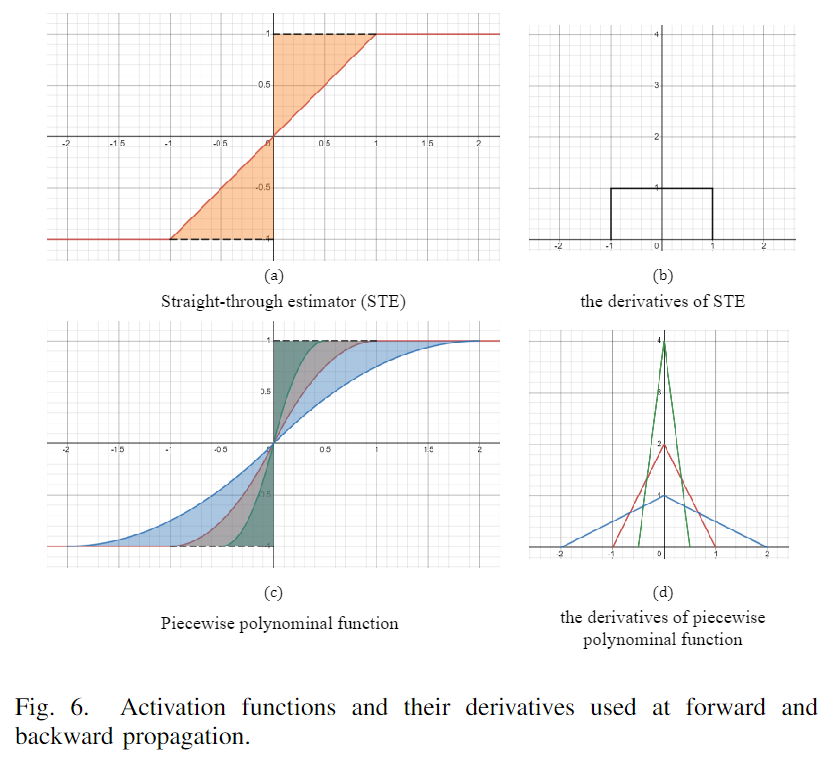
当梯度值超出剪切区间(见图6(b))时,梯度被截断为 0。sign 和 STE 之间大片的不匹配区域会影响学习的准确率。最近的方法设计近似可微函数来近似二值函数。如 Bi-Real Net 设计分段多项式函数作为近似函数(见图6©红线),其对应的导数如图6(d)。与STE的导数相比,分段多项式函数的导数更接近脉冲函数,使其在反向传播期间更有效地捕捉梯度信息。
对应的分段多项式函数和其导数如下:
$$
Appro(x) =
\begin{cases}
-1 &\text{if } x < 1 \
2x + x^2 & \text{if }-1 < x \leqslant 0 \
2x - x^2 & \text{if }0 < x \leqslant 1 \
1 & \text{otherwise}
\end{cases}
\tag{12}
$$
$$
\frac{\partial Appro(x)}{\partial x} =
\begin{cases}
2+2x &\text{if } -1 < x \leqslant 0 \
2-2x &\text{if } 0 < x \leqslant 1 \
0 &\text{otherwise}
\end{cases}
\tag{13}
$$
如上图6©所示,通过调整系数可以控制分段多项式函数。较大的剪切区间允许更多的位置通过近似函数,从而增强网络的更新能力。较小的剪切区间提高了梯度计算的准确性。本文专注于在早期训练阶段提高网络的更新能力,在随后的训练阶段提高网络的准确性,因此采用了从大到小的剪切区间。
对于较小的裁剪区间提高了梯度计算的准确性,GPT 解释如下:
剪切区间指的是对梯度进行截断或限制的范围。当这个范围较小时,即剪切区间较小,意味着梯度的取值范围受到了更强的限制。这可以使梯度计算更加精确,因为梯度值没有被放大到过大的程度,有助于更准确地追踪和反映网络参数的变化。
在训练神经网络时,梯度是一个关键的信号,用于指导参数的更新。较小的剪切区间可以确保梯度的变化不会太过剧烈,从而使得网络的学习过程更加稳定和可控。因此,通过选择较小的剪切区间,可以提高梯度计算的准确性,有助于网络更有效地学习和调整参数。
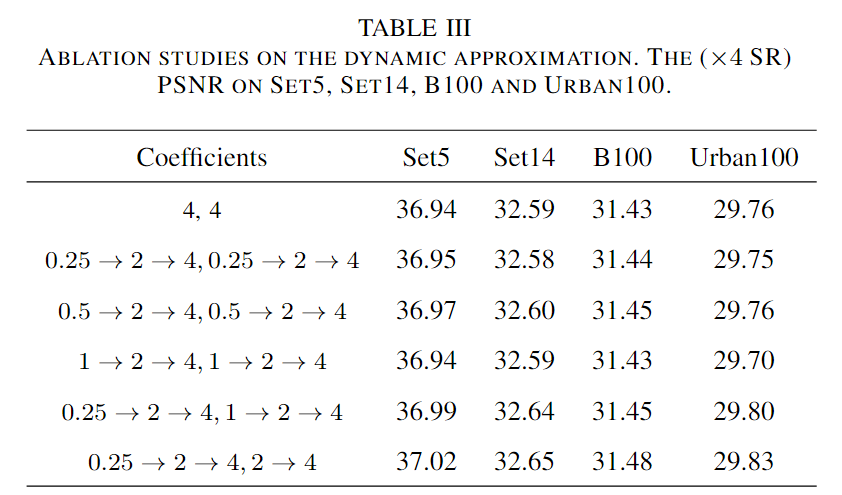
此外,考虑到高空间频率分布以0为中心,尾部迅速下降,而低空间频率分量的范围较宽,为低频分支分配了一个较小的初始系数。通过如下表III中对不同系数变化过程的探讨,最终选择低频分支的系数 $\delta$ 0.5-4(这里感觉是作者笔误,从表格来看应该是 0.25-4),高频分支的系数 2-4。
BinaryConv
不同的分支使用相同的二值处理过程。
在前向传播过程中,保留 sign 函数和实值尺度因子。
$$
Forward \space\space w^b=sign(w) \odot E(w) \tag{14}
$$
在反向传播中使用高阶估计器引导梯度更新。
$$
Backward \space\space \frac{\partial L}{\partial w} = \frac{\partial L}{\partial w^b} \cdot
\begin{cases}
4+8w &-0.5 < w \leqslant 0 \
4-8w &0 < w \leqslant 0.5\
0 &\text{otherwise}
\end{cases}
\tag{15}
$$
$w^b$ 表示二值权重。$E(w)$ 表示实值尺度因子,可以用 $\frac{1}{n}|w|_1$ 计算。$\odot$ 表示乘法操作。
全精度卷积可以被下面的二值卷积替代:
$$
w * x = sign(w) \otimes sign(x- \varepsilon) \odot E(w) \tag{16}
$$
$*$ 是卷积操作,$\otimes$ 是 bit-counting 卷积操作。
Activation
如下图4所示,LBRM 使用 PReLU 作为激活函数;HBRM 使用 recalibrated activation function(重校准激活函数)来提升 BNN 的表达能力。激活函数定义如下:
$$
y = \varphi \odot x + \varepsilon \tag{17}
$$
$$
\varphi, \varepsilon = F(x, \mathbb{W}_F) \tag{18}
$$
其中,$\varphi$ 和 $\varepsilon$ 是两组逐通道可学习的缩放因子,它们可以调整和偏移激活分布,使网络能够自适应地学习更适用于二值网络的分布。$W_F$ 是 $F$ 的参数,其计算方式如下:
Avg → FC → ReLU → Sigmoid
Structure
在低频分支中,主要目标是在前向传播过程中,保留网络中丰富的信息流,防止浅层特征的损失。为了实现这个目的,将 LBRM 的所有输出发送到网络的最后用于图像重建。此外,引入了一组可学习的系数来融合层次特征。处理过程如下:
$$
I^{LL’} = \delta_0 \odot I^{LL} + \sum_i^N\delta_i \odot I^{LL^i},i = 1,…,N \tag{19}
$$
$I^{LL^i}$ 表示低频分支的第 i 个 LBRM 输出。$\odot$ 表示乘法操作。N 表示 LBRM 的数量。
对于高频分支,保留简单的 residual block 堆叠结构。
Network
将模型扩展到四个不同的复杂程度:FABNet-B4C12, FABNet-B4C24, FABNetB4C36 和 FABNet-B8C96。
其中 B 表示 LBRM 的数量,2*B 表示 HBRM 的数量。C 表示 LBRM 的网络宽度,3*C 表示 HBRM 的网络宽度。
特别的,对于更轻量的网络结构 FABNet-B4C12, FABNet-B4C24 和FABNet-B4C36 中 LBRM 和 HBRM 全都保留 PReLU 作为激活函数。在 FABNet-B8C96 中,HBRM 保留 recalibrated 激活函数,LBRM 保留 PReLU。
5. EXPERIMENTS
- 数据集
使用 DIV2K 训练模型,使用 Set5, Set14, BSD100 和 Urban100 上的 ×2, ×3, ×4 做评估。
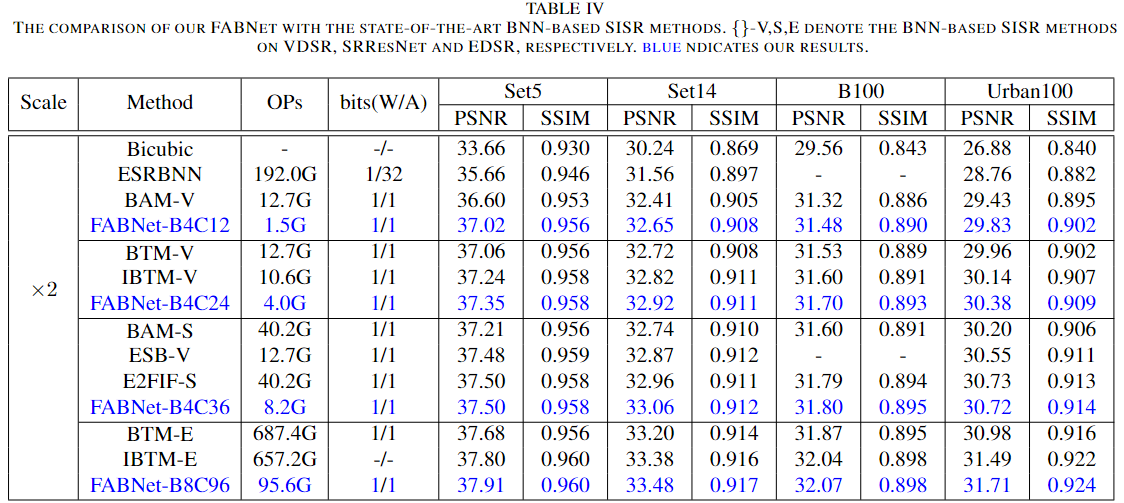
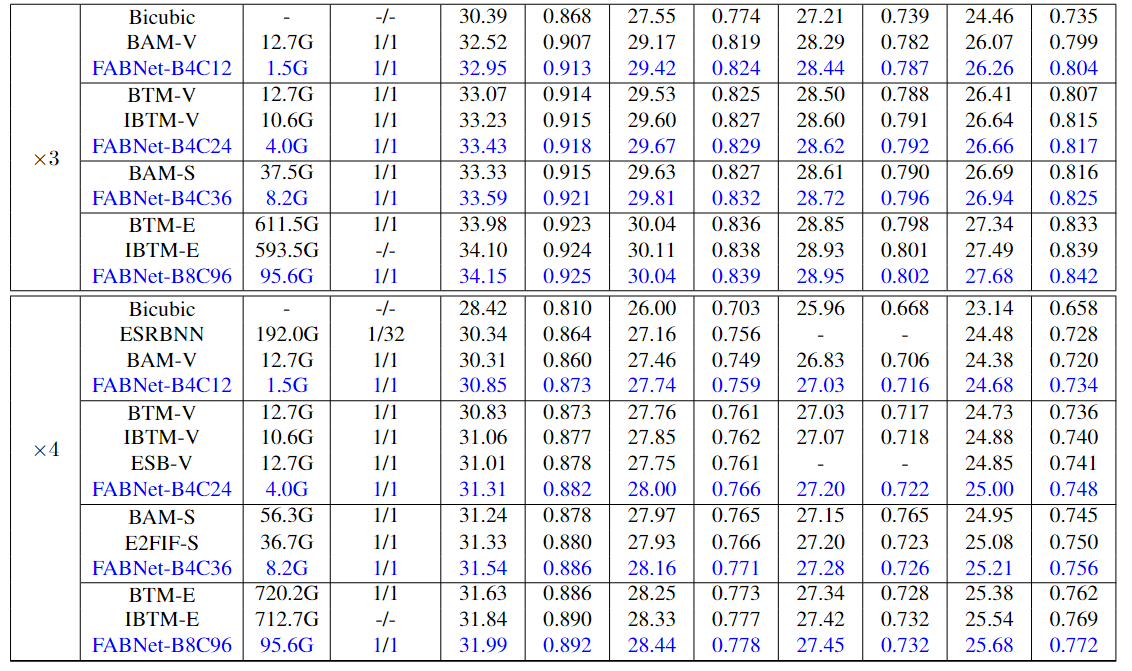
1) Comparison with the state-of-the-art BNN-based image SR methods
OPs are the sum of low-bit operations and floating-point operations.i.e., for 1-bit networks, OPs = BOPs/64 + FLOPs.
可视化比较效果如下:
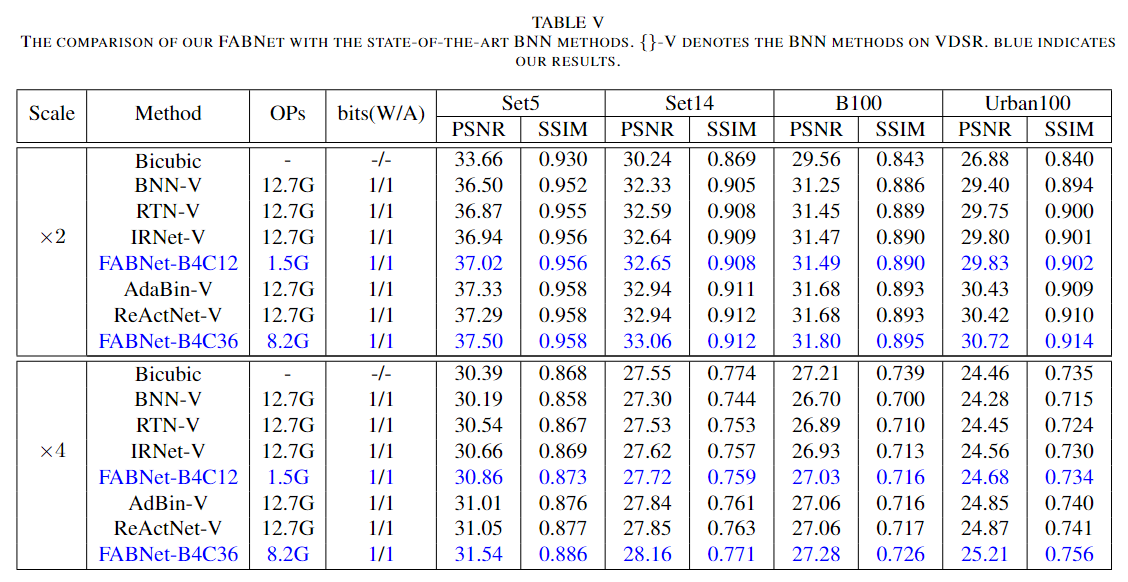
2) Comparison with the other state-of-the-art BNN methods
- Ablation Study
消融实验深入探讨了性能和参数之间的权衡,划分与征服策略的有效性,以及不同组件和系数对二值超分辨率网络性能的影响。
论文补充
- ReActNet: Towards Precise Binary Neural Network with Generalized Activation Functions
ReActNet 是基于 BNN 的网络,可以接近全精度网络的图像分类效果,回头研究一下作者怎么做的。