XNOR-Net: ImageNet Classification Using Binary Convolutional Neural Networks

这是 2016 年的文章。

代码地址(lua)： https://github.com/allenai/XnoR-Net/

python code : https://github.com/jiecaoyu/XNOR-Net-PyTorch

0. 摘要翻译

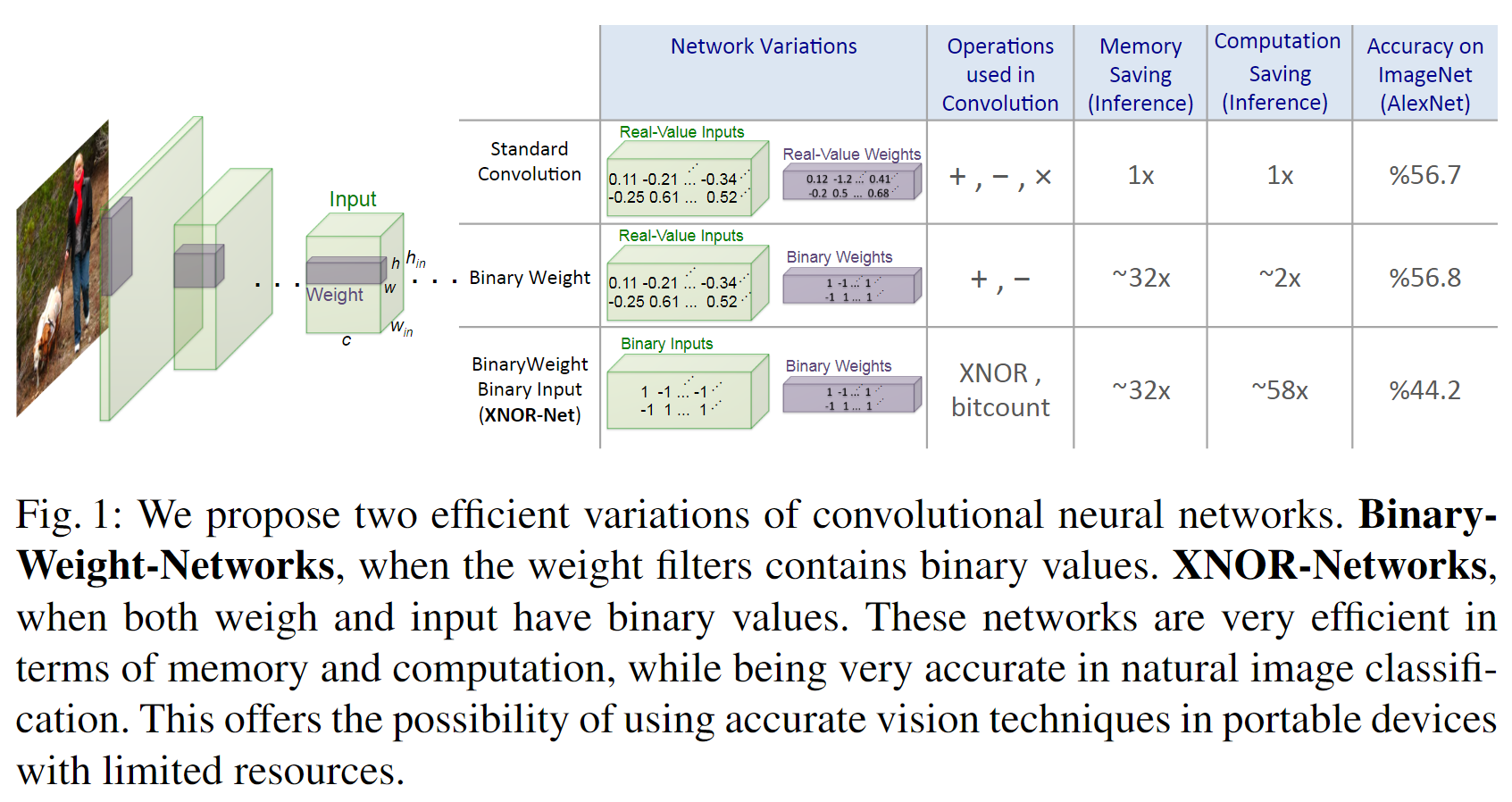
作者提出了两种有效的方法来近似标准卷积神经网络：Binary-Weight-Networks 和 XNOR-Networks。Binary-Weight-Networks 中，二值化的卷积核节省了 32 倍的内存。在 XNOR-Networks 中，过滤器和卷积层的输入都是二值化的。XNOR-Networks 使用简单的二元操作近似卷积。最终实现了 58 倍的卷积操作加速（相比高进度的操作数量）和 32 倍的内存节省。XNOR-Nets 提供了在 CPUs 上实时运行 SotA 的可能。作者在 ImageNet 分类任务上评估了该方。使用 AlexNet 二值化后的网络，其在图像分类任务上的准确率可以和全精度网络相同。作者比较了本文方法和 BinaryConnect 、BinaryNets ，在 ImageNets 上有大幅提升，top-1 的准确率提升了 16% 以上。

1. INTRODUCTION

本文作者贡献主要有两点：1.提出了一种二值化卷积网络权重值的方法，并与SotA方法进行了比较。2.介绍了 XNOR-Nets ，一个二值化了权重和输入的 DNN 模型，在推理更快内存更小的情况下取得了与标准图像分类网络近似的效果。

DNN 模型遭遇着过度参数化和大量的冗余的问题，导致计算和内存使用并不高效。下面是 2016 年以前的一些解决方法：

  • Shallow networks（浅层估计）：利用 DNN 先训练出一个模型，然后利用浅层网络模仿 DNN 的行为，从而实现浅层估计。
  • Compressing pre-trained deep networks：通过剪枝、Huffman (哈夫曼)编码、hash 函数、矩阵分解等方法进行模型压缩。
  • Designing compact layers：通过对不同的层设计小型的 block 、bottleneck 结构、将 3x3 的卷积核拆成 1x1 来去除冗余参数。
  • Quantizing parameters：通过更少位数的 integer 或者 二值 来替代 32-bit float ，从而轻量化网络。
  • Network binarization：二值化权重、激活。BinaryConnect 和 BinaryNet 在大数据集 ImageNet 上的表现不好。

3. 具体方法

用三元组表示 L层 CNN 的结构 $\langle \mathcal{I}, \mathcal{W}, \rangle$ 。$\mathcal{I}$ 是一组张量的集合，$\mathbf{I} = \mathcal{I}{l = 1, …, L}$ 是 $l^{th}$ 层 CNN 的输入张量（下图 Fig.1 中绿色块）。$\mathcal{W}$ 是也是张量集合，$\mathbf{W} = \mathcal{W}{lk(k=1,…,K^l)}$是 CNN 第 $l$ 层的第 $k$ 个权重 filter 。${K}^{l}$ 是 CNN 第 $l$ 层权重过滤器的数量。$$ 代表了 $\mathbf{I}$ 和 $\mathbf{W}$ 的卷积操作。$\mathbf{I} \in \mathbb{R}^{c \times w_{in} \times h_{in}}$ ，$(c, w_{in}, h_{in})$ 代表 channels，width 和 height。$\mathbf{W} \in \mathbb{R}^{c \times w \times h}$，其中$w \le w_{in}$，$h \le h_{in}$ 。作者提出了两种二值 CNN 的变体：

  • Binary-weights，$\mathcal{W}$ 的元素都是二值张量
  • XNOR-Networks，$\mathcal{I}$ 和 $\mathcal{W}$ 都是二值张量。

image-20231113152003493

3.1 Binary-Weight-Networks

为了把 CNN 约束成二值权重，通过二值的 filter $\mathbf{B} \in {+1, -1}^{c \times w \times h}$ 和一个缩放因子 $\alpha \in \mathbb{R}^{+}$ 来表示， $\mathbf{W} \approx \alpha \mathbf{B}$ 。卷积操作可以近似表示为：
$$
\mathbf{I} * \mathbf{W} \approx (\mathbf{I} \oplus \mathbf{B})\alpha \tag{1}
$$
$\oplus$ 表示无需任何乘法的卷积操作，由于权重是二值的，所以仅通过加减即可实现卷积。所以二值权重的卷积可以表示为 $\langle \mathcal{I}, \mathcal{B}, \mathcal{A}, \oplus \rangle$ 。$\mathcal{A}$ 是正实数尺度因子的集合。

Estimating binary weights:

求解 $\alpha$ 的过程

假设 $\mathbf{W}, \mathbf{B}$ 是 $\mathbb{R}^n$ 维度上的向量，$n = c \times w \times h$ ，通过如下的方式求解 $\alpha$ ：
$$
\begin{gathered}
{J}(\mathbf{B}, \alpha) = | \mathbf{W} - \alpha \mathbf{B} |^2 \
\alpha^, \mathbf{B}^ = \underset{\alpha, \mathbf{B}}{\operatorname{argmin}}J(\mathbf{B}, \alpha)
\end{gathered} \tag{2}
$$
将上式展开：
$$
J(\mathbf{B}, \alpha) = \alpha^{2}\mathbf{B}^\mathbf{T}\mathbf{B} - 2\alpha\mathbf{W}^\mathbf{T}\mathbf{B}+\mathbf{W}^T\mathbf{W} \tag{3}
$$
由于 $\mathbf{B} \in {+1, -1}^n$，$\mathbf{B}^\mathbf{T}\mathbf{B} = n$ 恒成立。$\mathbf{W}$ 也是个常数项。所以上式可以简化为
$$
J(\mathbf{B}, \alpha) = \alpha^2n - 2\alpha\mathbf{W}^\mathbf{T}\mathbf{B} + c
$$
所以要最小化 $J$ ，由于 $\alpha$ 是正的，那么就要最大化 $2\alpha\mathbf{W}^\mathbf{T}\mathbf{B}$
$$
\mathbf{B}^* = \underset{\mathbf{B}}{\operatorname{argmax}}{\mathbf{W}^\mathbf{T}\mathbf{B}} \space s.t. \mathbf{B}\in{+1, -1}^{n} \tag{4}
$$
要最大化上式，需要 $\mathbf{W}$ 的正值和负值的相反数相加，等价于
$$
\mathbf{B}^* = sign(\mathbf{W})
$$
有了最大的 $\mathbf{B}^$ ，求解最大的 $J$，对 $\alpha$ 求导，然后令导数为 0，求得
$$
\alpha^ = \frac{\mathbf{W}^\mathbf{T}\mathbf{B}^}{n} \tag{5}
$$
然后将 $\mathbf{B}^ = sign(\mathbf{W})$ 带入，得到
$$
\alpha^* = \frac{\mathbf{W}^\mathbf{T}sign(W)}{n} = \frac{\sum{|\mathbf{W}i|}}{n} = \frac{1}{n}|\mathbf{W}|{l_1} \tag{6}
$$
因此，对于最佳 $\mathcal{W}$ （二值权重）的评估可以简单的视为对权重使用 sign 函数。最佳尺度因子 $\alpha$ 就是权重绝对值的均值。

Training Binary-Weights-Networks:

CNN 的每一轮训练都包含三步：

  1. 前向传递
  2. 后向传递
  3. 参数更新

训练中，仅二值化前向和后向传播过程中的权重（在卷积层中）。

  • 计算 sign® 函数的梯度，遵循如下方式：

    $$
    \frac{\partial \operatorname{sign}}{\partial r} = r1_{|r| \le 1}
    $$

  • 缩放 $\alpha$ 后的 sign 函数在后向传播中的梯度如下：

    $$
    \frac{\partial C}{\partial W_i} = \frac{\partial C}{\widetilde W_i}(\frac{1}{n}+\frac{\partial sign}{\partial W_i} \alpha)
    $$

  • 更新权重使用高精度（实值）权重。

    因为在梯度下降过程中，参数的变化微小，更新后进行二值化将这些变化又被忽视了，训练的目标没有得到提升。

Algorithm 1解释了二值化权重的 CNN 训练过程：

  1. 通过在每一层计算 $\mathcal{B}$ 和 $\mathcal{A}$ 实现 weight filter 的二值化。此时前向传播使用二值权重和它相关的尺度因子，卷积运算为：
    $$
    \mathbf{I} * \mathbf{W} \approx (\mathbf{I} \oplus \mathbf{B}) \alpha
    $$

  2. 梯度是根据估计的 weight filters $\widetilde{\mathcal{W}}$ 计算的。

  3. 参数和学习率根据更新规则来更新，例如 momentum（向量法）或 ADAM 的 SGD 方法。

image-20231113210522458

3.2 XNOR-Networks

上面仅仅二值化了权重，这里来看将权重和输入全部二值化，从而可以利用 XNOR 和 bit-counting 来高效运算。

两个二值向量之间的点乘可以由 XNOR-Bitcounting 操作实现。首先，介绍如何使用二值操作实现两个二值向量之间的点积。然后，解释如何使用这种近似方法估计两个张量之间的卷积。

Binary Dot Product:

近似 $\mathbf{X}, \mathbf{W} \in \mathbb{R}^n$ 的点积操作：$\mathbf{X}^{\mathbf{T}}\mathbf{W} \approx \beta\mathbf{H}^{\mathbf{T}}\alpha\mathbf{B}$，其中 $\mathbf{H},\mathbf{B}\in {+1, -1}^n$ 并且 $\beta,\alpha\in\mathbb{R}^+$，所以要使近似误差最小：
$$
\alpha^,\mathbf{B}^,\beta^,\mathbf{H}^ = \underset{\alpha,\mathbf{B},\beta,\mathbf{H}}{\operatorname{argmin}}|\mathbf{X}\odot \mathbf{W}-\beta \alpha \mathbf{H} \odot \mathbf{B} |
\tag{7}
$$
$\odot$ 表示逐元素乘积。定义了 $\mathbf{Y} \in \mathbb{R}^n$ 比如 $\mathbf{Y}_i = \mathbf{X}_i \mathbf{W}_i$ ； $\mathbf{C} \in {+1, -1}^n$ 例如 $\mathbf{C}_i = \mathbf{H}_i \mathbf{B}_i$ ；$\gamma \in \mathbb{R}^+$ 例如 $\gamma = \beta \alpha$ 函数可以写成下式：
$$
\gamma^* , \mathbf{C}^* = \underset{\gamma, \mathbf{C}}{argmin}|\mathbf{Y} - \gamma \mathbf{C}|
\tag{8}
$$
类比公式$\eqref{eq2}$，可以通过求误差平方的导数为0时，对应的最值：
$$
\mathbf{C}^* = sign(\mathbf{Y}) = sign(\mathbf{X}) \odot sign(\mathbf{W}) = \mathbf{H}^* \odot \mathbf{B}^* \tag{9}
$$
同理 $\gamma^* = \frac{\sum{|\mathbf{Y}_i|}}{n}$，

由于 $|\mathbf{X}_i|,|\mathbf{W}_i|$ 是独立的，$\mathbf{Y}_i = \mathbf{X}_i \mathbf{W}_i$ ，所以 $\mathbf{E}[|\mathbf{Y}_i|] = \mathbf{E}[|\mathbf{X_i}||\mathbf{W}_i|] = \mathbf{E}[|\mathbf{X_i}|]\mathbf{E}[|\mathbf{W}_i|]$，因此
$$
\gamma^* = \frac{\sum{|\mathbf{Y}i|}}{n} = \frac{\sum{|\mathbf{X_i}||\mathbf{W}i|}}{n} \approx (\frac{1}{n}|\mathbf{X}|{\ell 1})(\frac{1}{n}\mathbf{W}{\ell 1}) = \beta^* \alpha^* \tag{10}
$$

Binary Convolution:

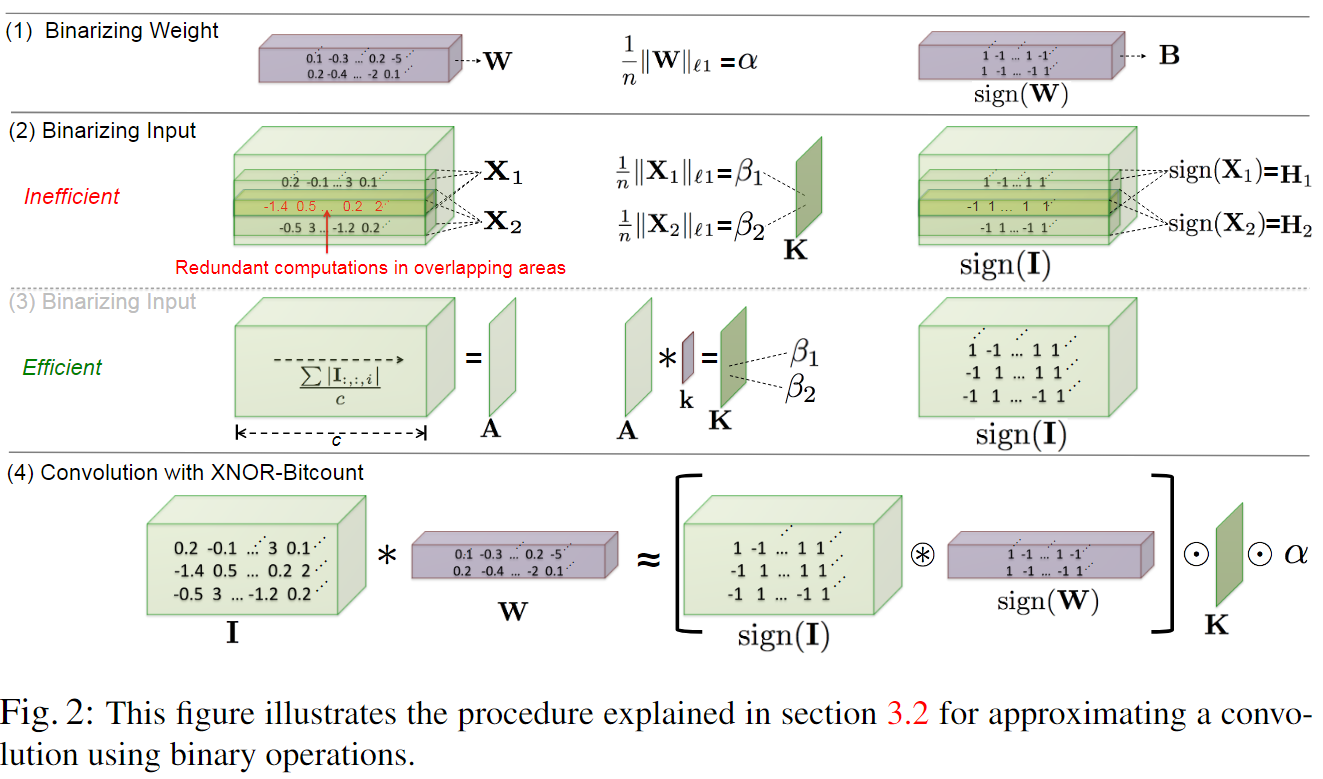
如下图，对于每个 weight filter 进行二值化，计算出一个 $\alpha$ 和 $\mathbf{B}$

对于每个输入，卷积操作是 weight filter 与其相应大小的 Input 进行卷积，要二值化输入，就需要对每个与 $\mathbf{W}$ 大小相同的子张量算出一个 $\beta$ 和 $\mathbf{H}$ ，不过从下图第二行可以看出，输入的子张量 $\mathbf{X}_1, \mathbf{X}_2$ 是有交集的，所以会在重复区域带来大量的冗余计算。

为了消除冗余计算，作者求出元素在通道上的绝对值的平均值 $\frac{\sum{I_:,:,i}}{c}$ ，得到一个矩阵 $\mathbf{A}$ ，然后将其与一个 2D filter $\mathbf{k}$ 进行卷积，其中 $\mathbf{k} \in \mathbb{R}^{w \times h}$ ，$\mathbf{K} = \mathbf{A} * \mathbf{k}$ ，其中 $\forall ij \space \mathbf{k}{ij} = \frac{1}{w \times h}$ 。$\mathbf{K}{ij}$ 表示 $\mathbf{I}$ 中以 i,j 为中心的子张量的相关的 $\beta$ 。

当我们获得了权重的缩放因子 $\alpha$ 和所有输入的子张量的 $\beta$ （用 $\mathbf{K}$ 表示），就可以二值操作来近似卷积了：
$$
\mathbf{I} * \mathbf{W} \approx (sign(\mathbf{I}) \circledast sign(\mathbf{W})) \odot \mathbf{K} \alpha \tag{11}
$$
$\circledast$ 表示使用 XNOR 和 bitcount 操作实现卷积。如下图最后一行所示。

image-20231114091819296

Training XNOR-Networks:

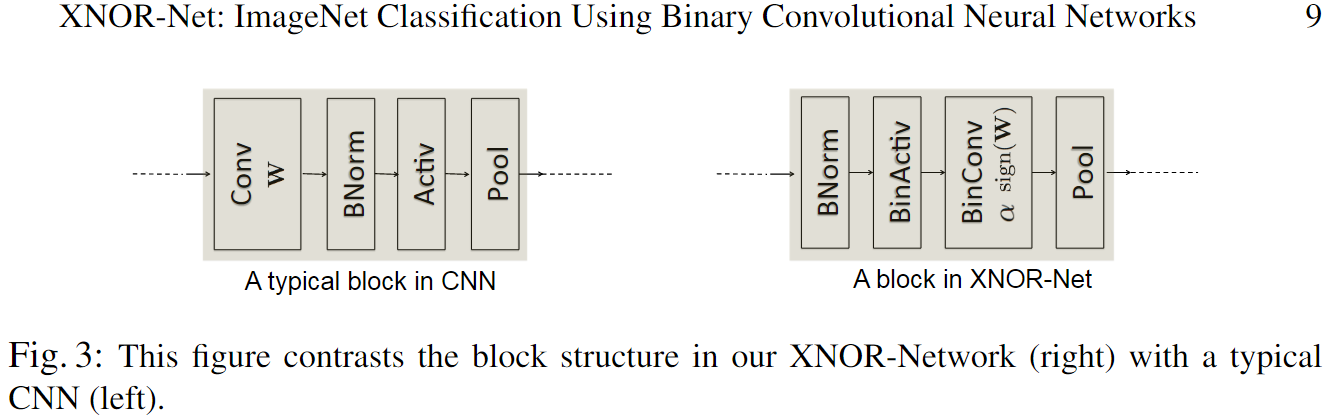
典型的 CNN 卷积 block 包含了一些不同的层，如下图左所示。

对于二值输入使用 max-pooling 得到的是一个大部分值为 +1 的张量，导致了大量的精度损失。于是将 pool 层放在卷积层之后，对输入先进行 normalize ，从而大幅减少二值化带来的信息损失。因为 BNorm 确保了数据以 0 为均值，将 0 作为阈值（-1， +1）会有更少的量化损失。所以二值 CNN 的 block 中，层间顺序如下图右所示。

The binary activation layer(BinActiv) 计算 $\mathbf{K}$ 和 $sign(\mathbf{I})$ 。然后在 BinConv 层中进行如下运算：
$$
\mathbf{I} * \mathbf{W} \approx (sign(\mathbf{I}) \circledast sign(\mathbf{W})) \odot \mathbf{K} \alpha
$$
最后是 pool 层，可以在 BinConv 之后插入非二值的激活（如 ReLU）。这在使用 SotA（如 AlexNet 或 VGG）上是有用的。

image-20231114120556881

Binary Gradient:

反向传播中的计算瓶颈是 weight filters($w$) 和 关于输入($g^{in}$)的梯度之间的卷积。这里类比前向传播，二值化输入($g^{in}$)。注意如果利用公式$\eqref{eq6}$计算缩放因子，会导致 SGD 的最大变化方向衰减。为了保留最大的变化方向，使用 $max_i{|g_i^{in}|}$ 作为尺度因子。

k-bit Quantization:

上面二值化的方法是量化为 1bit，但是用下面的式子很容易可以量化为 k-bit。（式子我没看懂。）
$$
q_k(x)=2(\frac{[(2^k-1)(\frac{x+1}{2})]}{2^k-11}-\frac{1}{2})
$$
其中 [.] 表示舍入操作，$x \in [-1, 1]$ 。

4. 实验

这是第一篇将二值网络应用在 ImageNet 数据上的工作。本文的二值化方法具有普适性，可应用在任何 CNN 结构上。

作者还与 BinaryConnect 和 BinaryNet 进行了比较。

消融实验评估了计算尺度因子和用于二值化 CNN 的 block 结构 的作用。

4.1 Efficiency Analysis

在标准卷积中，总的操作数是 $cN_WN_I$ ，$c$ 是通道数，$N_W = wh$ 并且 $N_I = w_{in}h_{in}$ 。现代 CPU 有些可以把加法和乘法融合在一个循环中，这时 Binary-Weight-Networks 的权重就没什么提升了。本文对卷积的二进制近似有 $cN_WN_I$ 次二进制运算，和 $N_I$ 次非二进制运算。64位 CPU 可以在一个时钟周期中实现 64 次二进制运算。因此，速度提升可以近似为
$$
S = \frac{cN_WN_I}{\frac{1}{64}cN_WN_I+N_I} = \frac{64cN_W}{cN_W + 64}
$$
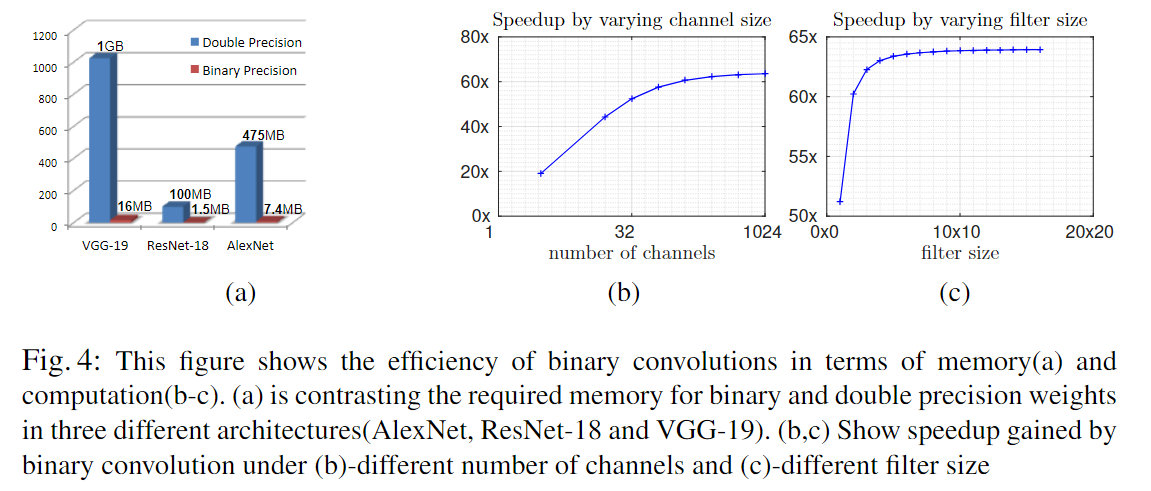
由速度的提升与 channel size 和 filter size 有关，但是和 input size 无关。如下图 b,c ,修改一个 size 大小时，设置其他的大小为 $c = 256,n_I = 142, n_W = 32$ （大部分 ResNet 中的卷积结构是这样设置的）。本文的卷积近似方法，理论上可以实现62.27倍的加速，但是实际在CPU上一个卷积实现了58倍的加速（不包括内存分配和内存访问过程）。使用小的通道尺寸（c = 3）和 filter size（$N_W = 1 \times 1$）加速并不明显。这激励作者没有对第一层和最后一层CNN进行二值化。

image-20231114193654940

本文提出方法的主要不同是使用了缩放因子，在没有改变效率顺序的情况下还带来了准确性的提升。

4.2 Image Classification

作者使用 Top1 和 Top5 的准确性反应性能。作者采用了三种不同的CNN架构作为二值化的基础：

AlexNet，ResNet，以及 GoogLenet 的变体。

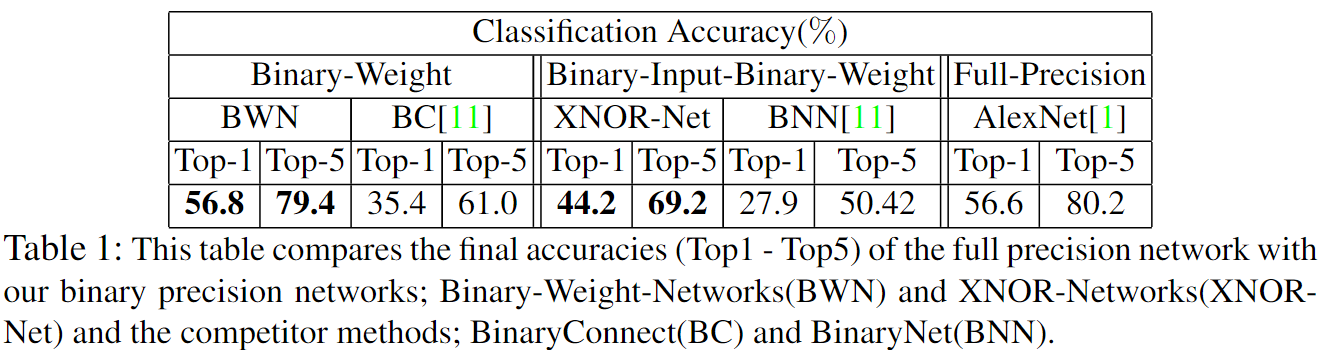
作者比较了 Binary-Weight-Networks(BWN) 和 BinaryConnect（BC）。以及 XNOR-Networks(XNOR-Net) 和 BinaryNeuralNet(BNN)。

  • BC: 在前向传播和反向传播中二值化了权重，但参数更新过程保留了实数。
  • BNN: 在推理（inference）阶段和训练中的梯度计算过程中使用二进制（binary）的权重和激活值。

AlexNet

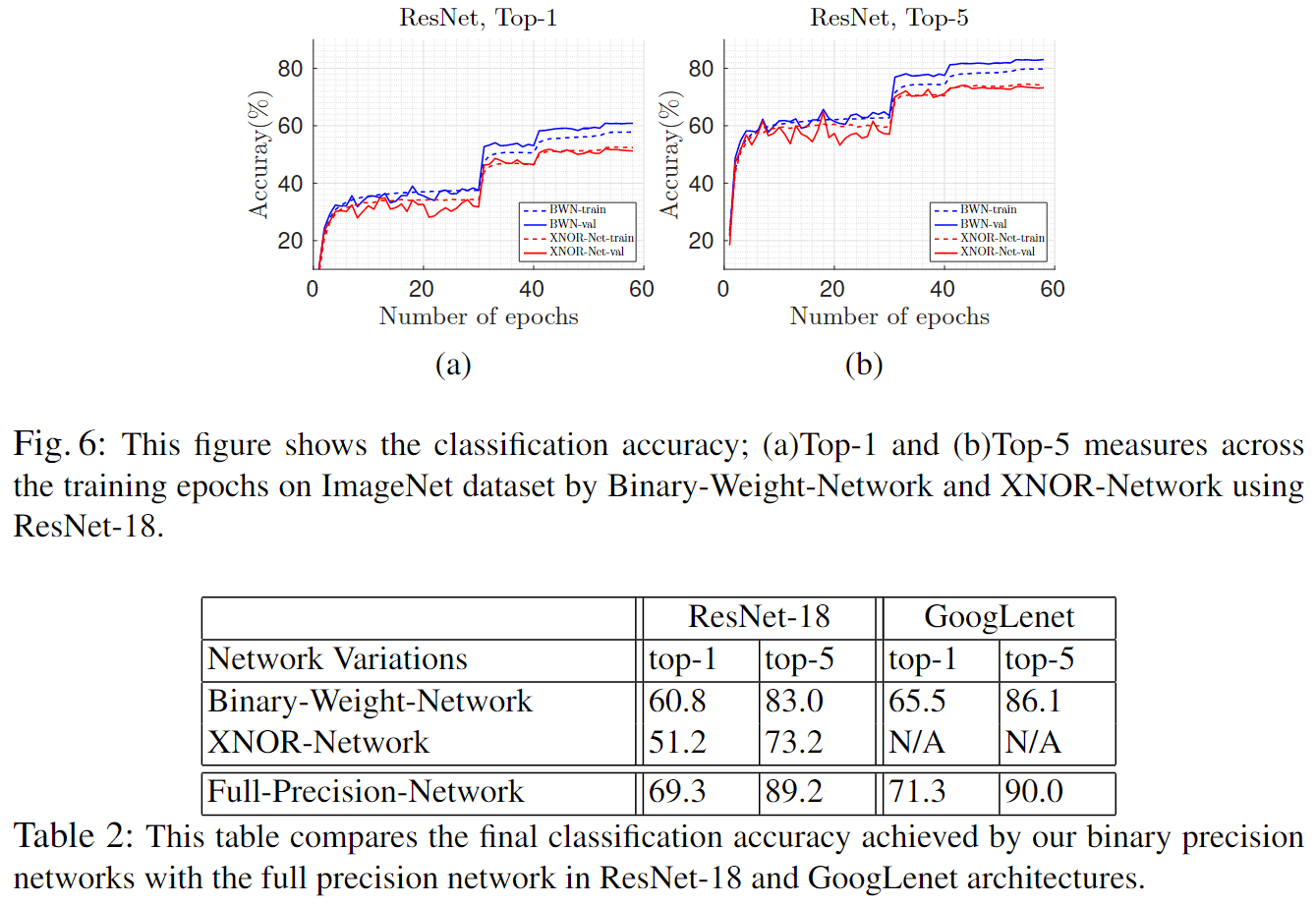
下图表展示了随着训练周期的增加，训练和推断（inference）阶段的分类准确度，分别对应了top-1和top-5分数。

"Top-1"和"Top-5"通常用于评估分类任务的性能，它们分别表示模型在选择最有可能的类别时的准确度（Top-1），以及在考虑前五个最可能的类别时的准确度（Top-5）。

image-20231114214951356

下表展示了最终的对比结果。

image-20231114215243170

权重的尺度因子 $\alpha$ 带来的精度提升更大（~17%），而输入的尺度因子带来的精度提升很小（在 AlexNet 上不到 1%）。

ResNet

image-20231114220042755

4.3 Ablation Studies

本文比较以往方法的不同：

  • 二值化的方法

    在训练迭代中找到的最优比例因子。

  • 二值CNN中的block结构

    通过 block 的顺序来降低训练 XNOR-Net 过程中的量化损失。

其实就是将传统方法直接二值，和本文二值方法做对比，本文效果更好。

image-20231114220415356

需要补充补充了解的论文

  • Cross-domain synthesis of medical images using efficient location-sensitive deep network.

    这篇 2015 的文章中介绍了如何二值化激活。（帮助了解如何二值化激活，已经理解激活是什么）

  • Deep Compression: Compressing Deep Neural Networks with Pruning, Trained Quantization and Huffman Coding

    2015：学习哈夫曼编码在模型压缩中的应用

  • Compressing Neural Networks with the Hashing Trick

    2015：学习Hash在模型压缩中的应用

  • 这篇文章不错：https://aijishu.com/a/1060000000093054

    讲了 BNN → XNOR-Net → Bi-RealNet → BinaryDenseNet → MeliusNet 的改进过程。