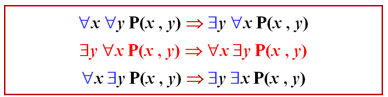人工智能复习（二）

三、推理

1. 推理的基本概念

推理就是按照某种策略从已有事实和知识推出结论的过程。

按推理的逻辑基础分类

  1. 演绎推理

    从已知的一般性知识出发，推理出适合于某种个别情况的结论过程。
    即从一般到个别的推理。
    常用形式：三段论法(大前提、小前提、结论)

    大前提：是已知的一般性知识或推理过程得到的判断；
    小前提：是关于某种具体情况或某个具体实例的判断；
    结论：是由大前提推出的，并且适合于小前提的判断。

    image-20221112224143886

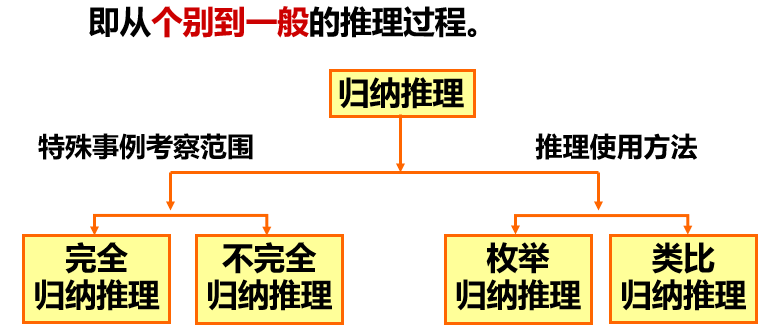
  2. 归纳推理

    从大量特殊事例出发，归纳出一般性结论的推理过程。

    image-20221112224242848

按所用知识的确定性分类

  1. 确定性推理

    推理时所有用的知识和证据都是确定的，推出的结论也是确定的，其真值或者为真或者为假，没有第三种情况出现。

  2. 不确定性推理

    推理时所用的知识和证据不都是确定的，推出的结论也不确定的。

按推理中所用知识是否具有启发性分类

  1. 启发式推理

    推理过程中应用与问题有关的启发性知识，即解决问题的的策略、技巧及经验，以加快推理过程，提高搜索效率。

  2. 非启发式推理

    在推理过程中，不运用启发性知识，只按照一般的控制逻辑进行推理。这种方法缺乏对求解问题的针对性，所以推理效率较低，容易出现“组合爆炸”问题。

推理的控制策略

推理的控制策略是指如何使用领域知识使推理过程尽快达到目标的策略。

  • 由于智能系统的推理过程一般表现为一种搜索过程，因此，推理的控制策略又可分为推理策略和搜索策略。

    • 推理策略

      推理方向控制策略用于确定推理的控制方向，可分为正向推理、逆向推理、混合推理及双向推理。

      求解策略是指仅求一个解，还是求所有解或最优解等。

      限制策略是指对推理的深度、宽度、时间、空间等进行的限制。

      冲突消解策略是指当推理过程有多条知识可用时，如何从这多条可用知识中选出一条最佳知识用于推理的策略。

  • 搜索策略

    • 主要解决推理线路、推理效果、推理效率等问题。

2. 确定性/谓词逻辑推理

2.1 谓词逻辑基础介绍

  • 谓词的真假，谓词公式的等价性，永真蕴含式，置换与合一

  • $a⊕b = (¬a ∧ b) ∨ (a ∧¬b)$

  • image-20221113120750212

    image-20221113120807284

    image-20221113120822166

    image-20221113120837388

    image-20221113120922424

    image-20221113121909964

    image-20221113122019661

    image-20221113122206768

    image-20221113122332827

  • 置换与合一

  • image-20221113123106514

  • image-20221113123007632

  • image-20221113123325397

    image-20221113123801261

    即删去（1）分子分母相除为1的结果，（2）删除 $\theta$ 和 $\lambda$ 中共有的分母

  • image-20221113124315580

  • image-20221113124440362

    image-20221113124615181

  • image-20221113130217646

    image-20221113130241204

    image-20221113130251806

    image-20221113130302155

    image-20221113130312441

2.2 谓词逻辑的自然演绎推理（重点）

从一组已知为真的事实出发，直接运用命题逻辑或谓词逻辑中的推理规则推出结论的过程。

最基本的推理规则有：

  1. 假言三段论

image-20221113130723052

  1. 假言推理

image-20221113130736600

  1. 拒取式

image-20221113130821140

image-20221113131040596

image-20221113131249942

image-20221113132010112

2.3 谓词逻辑的归结演绎推理（重点）

归结原理除了可用于定理证明外，还可用来求取问题答案,其思想与定理证明相似。

下面给出求取问题答案的一般步骤:

(1)把问题的已知条件用谓词公式表示出来,并化为相应的子句集;

(2)把问题的目标的否定用谓词公式表示出来,并化为子句集;

(3)对目标否定子句集中的每个子句,构造该子句的重言式(即把该目标否定子句和此目标否定子句的否定之间再进行析取所得到的子句),用这些重言式代替相应的目标否定子句式,并把这些重言式加人到前提子句集中,得到一个新的子句集;

(4)对这个新的子句集,应用归结原理求出其证明树,这时证明树的根子句不为空,称这个证明树为修改证明树;

(5)用修改证明树的根子句作为回答语句.则答案就在此根子句中。

  • 子句集的化简步骤
    1. 消去连接词
    2. 减少否定符号的辖域
    3. 对变元标准化
    4. 化为前束范式
    5. 消去存在量词
    6. 化为Skolem标准形
    7. 消去全称量词
    8. 消去全称量词
    9. 更换变量名称

image-20221113164530578

image-20221113164553499

image-20221113164606050

image-20221113164619815

image-20221113164636269

例题：

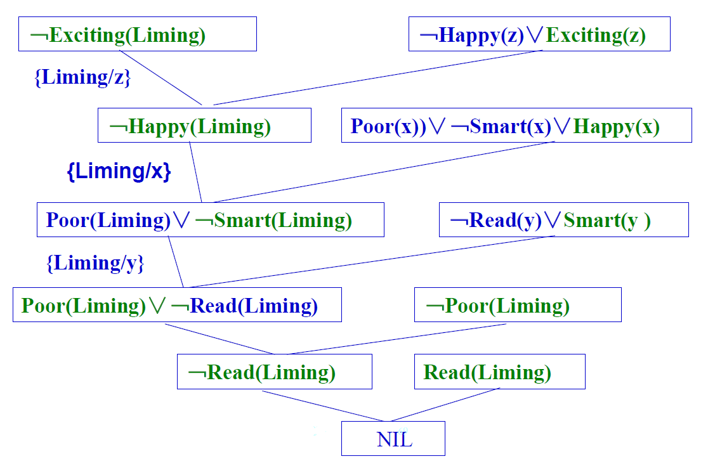
已知：张和李是同班同学，如果x和y是同班同学，则x的教室也是y的教室，现在张在302教室，上课。

问：现在李在哪个教室上课？

解：

  • 首先定义谓词：

    $C(x, y)$ x和y是同班同学；

    $A1(x, u)$ x在u教室上课。

  • 把已知前提用谓词公式表示如下:

    $C(zhang，li)$

    $(\forall r)(\forall y)(\forall u)(C(x, y) \wedge At(x, u) \rightarrow At(y, u))$

    $At(zhang, 302)$

  • 把目标的否定用谓词公式表示如下：

    $\neg (\exists v)At(li, v)$

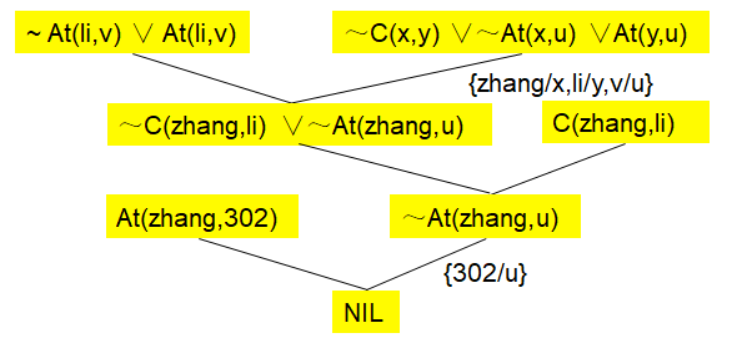
  • 把上述公式化为子句集：

    $C(zhang, li)$

    $\neg C(x, y) \vee \neg At(x，u) \vee At(y, u)$

    $At(zhang,302)$

  • 把目标的否定化成子句式，并用重言式

    $\neg At(li, v) \vee At(li,v)$

    image-20221113154030832

2.3.1 命题逻辑的归结反演

image-20221113160323882

例题1

image-20221113160407490

2.3.2 谓词逻辑的归结演绎推理

image-20221113160742702

image-20221113160756059

image-20221113160809344

归结演绎的经典例子：

image-20221113160933236

image-20221113160943539

image-20221113160954390

image-20221113161005288

归结反演求取答案的例子：

image-20221113161412442

image-20221113161429988

image-20221113161445335

image-20221113161510936

image-20221113161538525

再来一题

image-20221113161931562

image-20221113161940715

image-20221113161951692

  • 归结策略

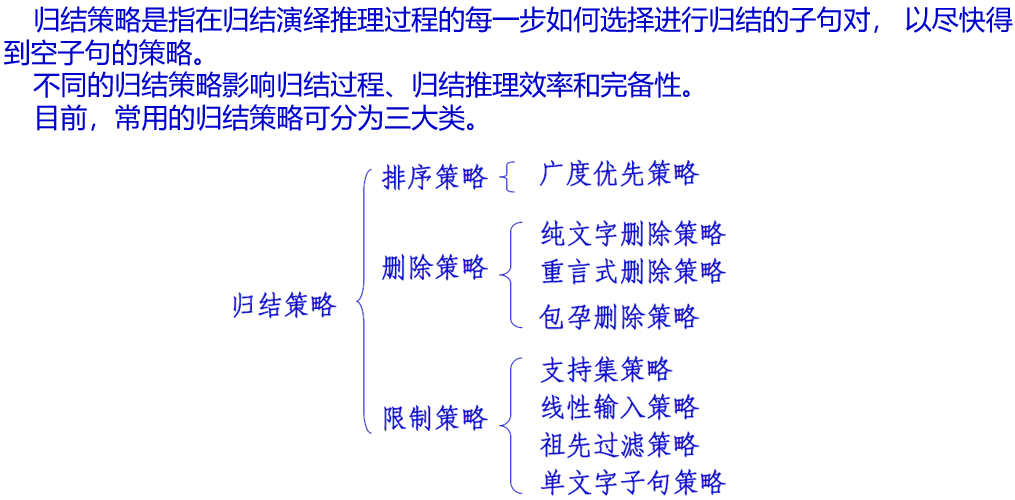
image-20221113161734495

3. 不确定性推理

从不确定性的初始证据出发，通过运用不确定性的知识，最终推出具有一定程度的不确定性但却是合理或者近乎合理的结论的思维过程。

3.1 不确定性推理的分类

  • 不确定性推理中的基本问题
    1. 不确定性的表示与量度
    2. 不确定性匹配算法及阈值的选择
    3. 组合证据不确定性的算法
    4. 不确定性的传递算法
    5. 结论不确定性的合成
  • 证据理论
    1. 概率分配函数
    2. 信任函数
    3. 似然函数
    4. 概率分配函数的正交和（证据的组合）
    5. 基于证据理论的不确定性推理

实战练手

例题1

证明G是否为F1, F2的逻辑结论。

$F1: (∀x)(P(x)→(∀y)(Q(y)→﹁L(x.y)))$ ，
$F2:  (∃x)(P(x)∧(∀y)(R(y)→L(x.y)))$
$G:   ( ∀x)(R(x)→﹁Q(x))$

解：

  1. 先把 G 否定，放入与 F1， F2 放在一起

    ${F1, F2, \neg G}$

  2. 把 ${F1, F2, \neg G}$ 化为子句集

    1. $\neg P(x) \vee \neg Q(y) \vee \neg L(x,y)$
    2. $P(m)$
    3. $\neg R(m) \vee L(m,n)$
    4. $R(u)$
    5. $Q(v)$

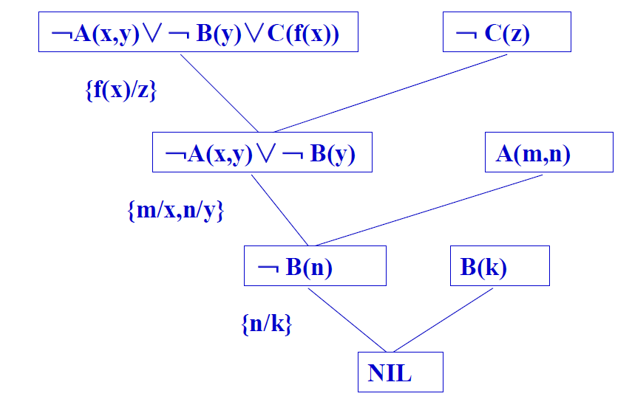
  3. 对上式进行归结

    1 与 2 归结，取 $\sigma = {m/x,n/y}$

    1. $\neg Q(n) \vee \neg L(m, n)$

    3 与 6 归结

    1. $\neg R(m) \vee \neg Q(m)$

    4, 5, 7 归结，取 $\sigma = {u/m, v/n}$

  4. 最终归结为 NIL

因此，G 是 F1, F2 的逻辑结论。

例题2

三、张某被盗，公安局派出五个侦探去调查．研究案情时，侦察员A说＂赵与钱中至少有一人做案＂；侦察员B说＂钱与孙中至少有一人做案＂；侦察员C说＂孙与李中至少有一人做案＂；侦察员D说＂赵与孙中至少有一个与此案无关＂；侦察员E说＂钱与李中至少有一人与此案无关＂。 如果这五个侦察员的话都有是可信，请用归结原理求出谁是盗窃犯。

解：

(1) 先定义谓词和常量 
设C(x)表示x作案，Z表示赵，Q表示钱，S表示孙，L表示李

(2) 将已知事实用谓词公式表示出来 
赵与钱中至少有一个人作案：$C(Z)∨C(Q)$
钱与孙中至少有一个人作案：$C(Q)∨C(S)$
孙与李中至少有一个人作案：$C(S)∨C(L)$ 
赵与孙中至少有一个人与此案无关： $¬C (Z) ∨¬C(S)$
钱与李中至少有一个人与此案无关： $¬C (Q) ∨¬C(L) $

(3) 将所要求的问题用谓词公式表示出来，并与其否定取析取。 设作案者为u，则要求的结论是C(u)。将其与其否)取析取，

得：$¬C(u) ∨C(u)$

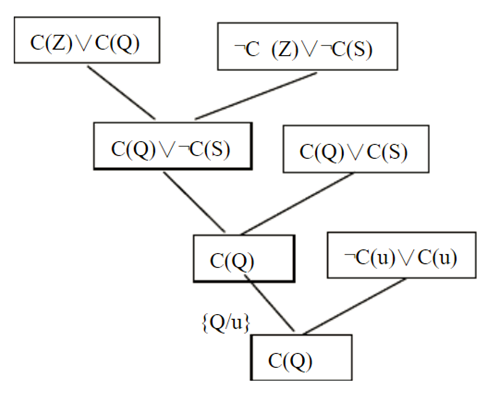
(4) 对上述扩充的子句集，按归结原理进行归结，其修改的证明树如下：

image-20221123131052380

因此，钱是盗窃犯。

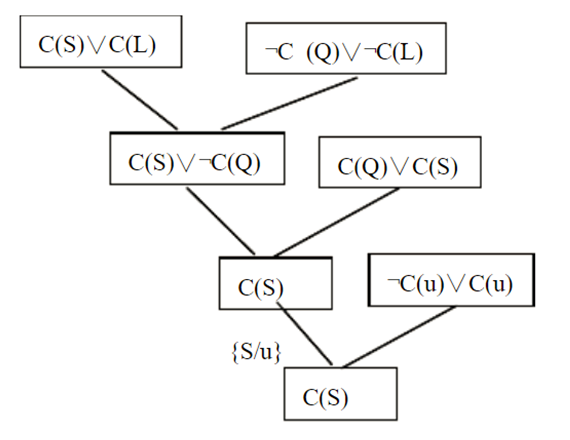
实际上，本案的盗窃犯不止一人。根据归结原理还可以得出：

image-20221123131116242

因此，孙也是盗窃犯。