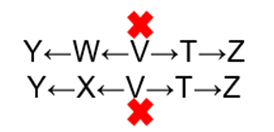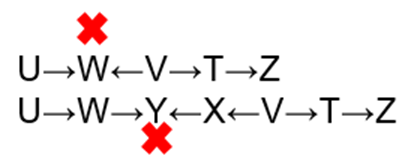人工智能(三)
人工智能复习(三)
三、推理
3. 不确定性推理
3.2 概率推理(Bayes 是重点)
3.2.1 概率的基础介绍
- 理解随机变量
- 联合概率,边缘概率,条件概率的意义及计算方法
- 链式法则及贝叶斯法则
3.2.2 贝叶斯网络的表示(重点)
- 贝叶斯网络的表示方法,其中任意两个节点间相互独立性的判断方法
贝叶斯网(Bayesian network)亦 称 “信念网”(belief network),它借助有向无环图(Directed Acyclic Graph ,简 称 DAG)来刻画属性之间的依赖关系,并使用条件概率表(Conditional Probability Table ,简 称 CPT )来描述属性的联合概率分布。
贝叶斯网结构有效地表达了属性间的条件独立性。
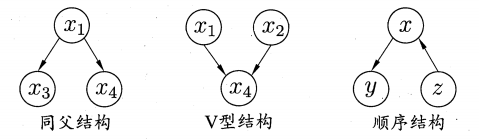
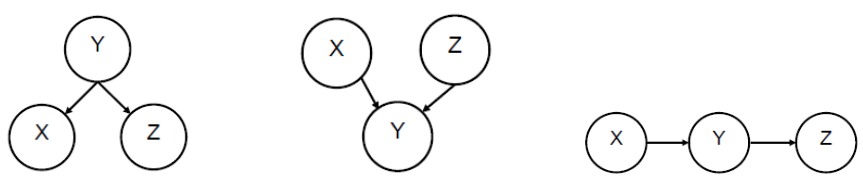
贝叶斯网络中的三种典型关系:
- 同父结构:$x_1$ 确定时,$x_3,x_4$ 条件独立
- V 型结构:$x_4$ 不确定时,$x_1,x_3$ 条件独立
- 顺序结构:$x$ 确定时,$y, z$ 条件独立
判断条件独立时,有两种方法:
- D分离(D-Seperation):如果前提条件判断两个变量 $a, b$ 是否独立:则将有向图做节点合并,缩成两个大的节点和一个关键节点,这样就可以通过上面三种结构判断 $a, b$ 各自所在的集合是否独立。如果所在集合独立,则 $a,b$ 独立;否则继续划分,直到能够判断 $a,b$ 独立或者相关。
- 道德图:如果给定前提条件判断两个变量 $a,b$ 是否独立:则找出图中所有的 V 型结构,将父节点用无向边相连,然后将图中所有的有向边变为无向边,此为道德图。如果去掉前提条件节点后 $a,b$ 之间无连边,则独立;否则说明在该前提条件下 $a,b$ 不独立。
例题1
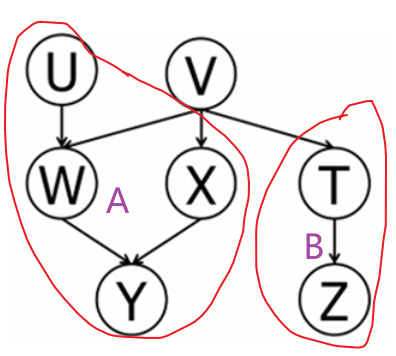
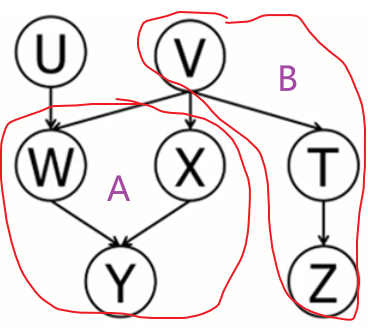
基于下图贝叶斯网络,判断以下表达是否为真。若不为真,请给出任意一条激活(不相互独立)的路径;若为真,给出所有路径并标出每条路径不激活的位置。
解:
(1)无前提条件判断独立:使用 D-Seperation :划分完节点如下图,是一个同父结构,V未知,所以集合 A,B 独立,故 Y,Z 独立。
激活路径有Y←W←V→T→Z
(2)有前提条件判断独立:使用道德图:对所有的 V 型结构父节点连线,去掉条件 X 节点后,Y 与 Z 仍连接,所以 X 条件下,Y,Z 不独立。激活路径有Y←W←V→T→Z
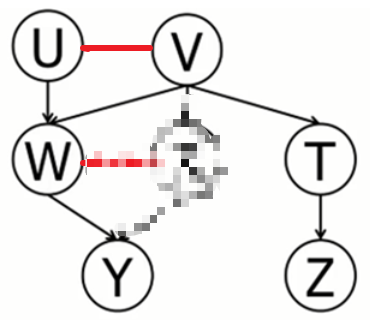
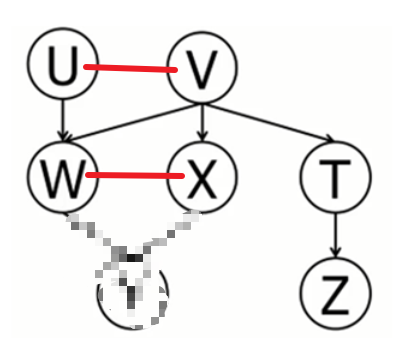
(3)有前提条件判断独立:使用道德图:如下图,在 V 已知的条件下 Y,Z 独立。
路径如下:
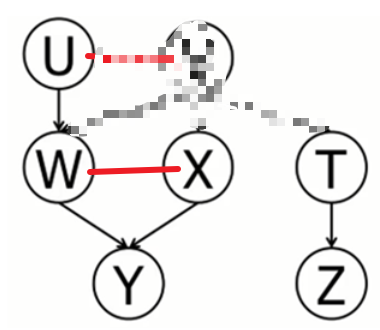
(4)无前提条件判断独立:使用 D-Seperation :如下图,A 集合未知,U、A、B 构成了 V 型结构,即 U、B 独立,故 U,Z 独立。
路径如下:
(5)有前提条件判断独立:使用道德图:如下图,在 Y 已知的条件下 U,Z 不独立。
激活路径有U→W←V→T→Z
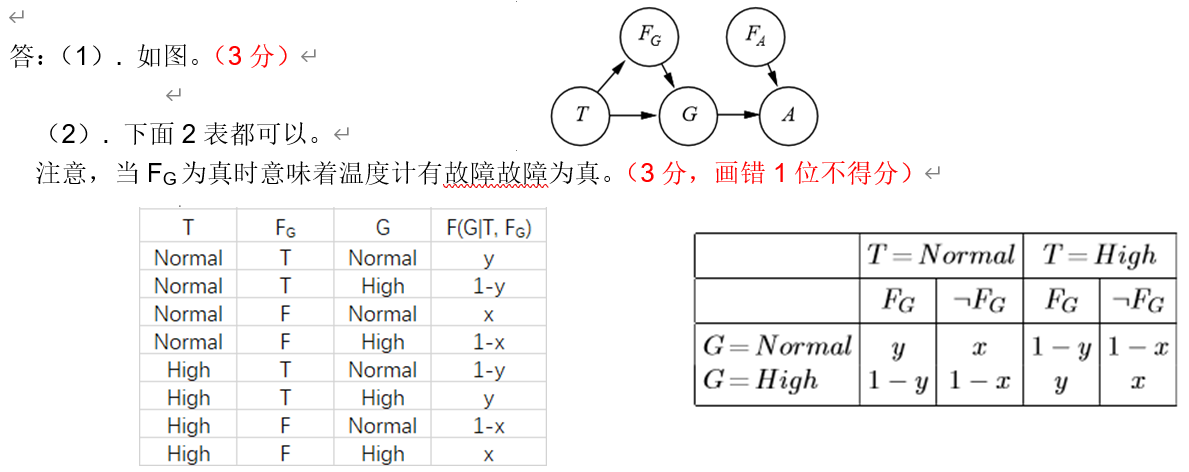
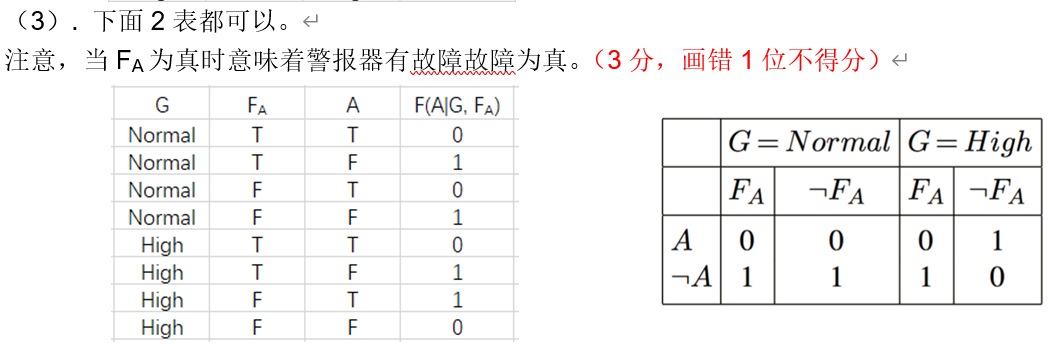
例题2
3.2.3 贝叶斯网络的精确及近似推理(重点)
实现原理
举例说明
目标是求出
$$
P(X|A,B)
$$
基础知识准备
由Bayes公式
$$
P(A|B) = \frac{P(B|A)*P(A)}{P(B)}
$$
由联合概率分布公式
$$
P(A,B)= P(A|B)*P(B)
$$
推广一下
$$
P(X_1,X_2,…,X_n) = P(X_1|X_2,…,X_n)P(X_2|X_3,…,X_n)…*P(X_n)
$$
当$X_1,X_2,X_3,…,X_n$之间相互影响时,有上式
如果$X_1$和$X_2$独立,那么上面得公式中
$$
P(X_1|X_2,…,X_n) = P(X_1|X_3,…,X_n)
$$
上式是我们通过Bayes网络中的先验概率求得联合概率的关键
Bayes网络就是一个有向无环图,每个节点被指向它的节点影响,而和无法相互到达的节点相互独立
上图右一中,$X$和$Z$不是相互联系的,但是当$Y$的值确定下来后,$X$和$Z$相互独立。再Bayes网络中,每个节点的CPT都是可求的,再求到字节点的CPT之前,其父节点的CPT已经变成已知,于是可以认为每个节点只受其直接父节点的影响。
这样求解某个节点事件的发生概率就变成了,求在其直接父节点发生的情况下,该节点事件发生的概率
即Bayes网络中的事件联合概率分布可以使用如下方法求解
$$
P(A,B,C,…) = P(A|A’s\space fathers)*P(B|B’s\space fathers)P(C|C’s\space fathers)…
$$
于是Bayes公式可以简化为
$$
P(A|B) = \frac{P(B|A)*P(A)}{P(B)} = \frac{P(A,B)}{P(B)} = \frac{P(A,B)}{P(B|A)+P(B|\neg A)}
$$
目标式可以转化为
$$
P(X|A,B)=\frac{P(X,A,B)}{P(A,B)} = \frac{P(X|X’s\space fathers)*P(A|A’s\space fathers)*P(B|B’s\space fathers)}{P(A|A’s\space fathers)*P(B|B’s\space fathers)}
$$
如果网络中还有事件$C、D$,计算联合概率时,带入一同计算即可(由于这里建立的CPT表是一张包含所有组合情况的表)
$$
P(X|A,B)=\frac{P(X,A,B,C,D)}{P(A,B,C,D)}+\frac{P(X,A,B,\neg C,D)}{P(A,B,\neg C,D)}+\frac{P(X,A,B,C,\neg D)}{P(A,B,C,\neg D)}+\frac{P(X,A,B,\neg C,\neg D)}{P(A,B,\neg C,\neg D)}
$$
利用上式进行Bayes网络对特定事件结果的预测
贝叶斯网络中条件概率的计算方法
- 贝叶斯网络中条件概率的计算方法(枚举法以及变元消除法)
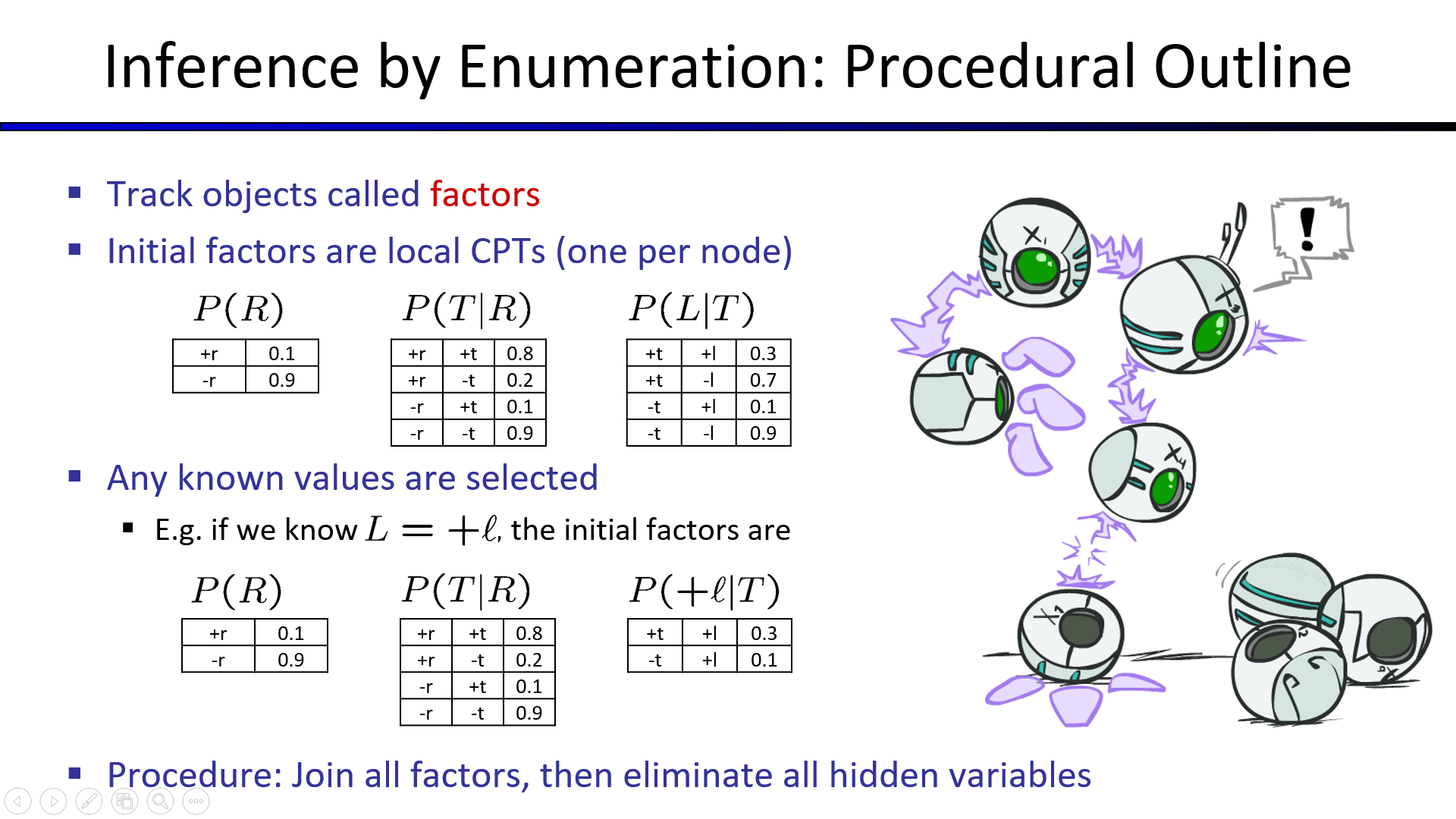
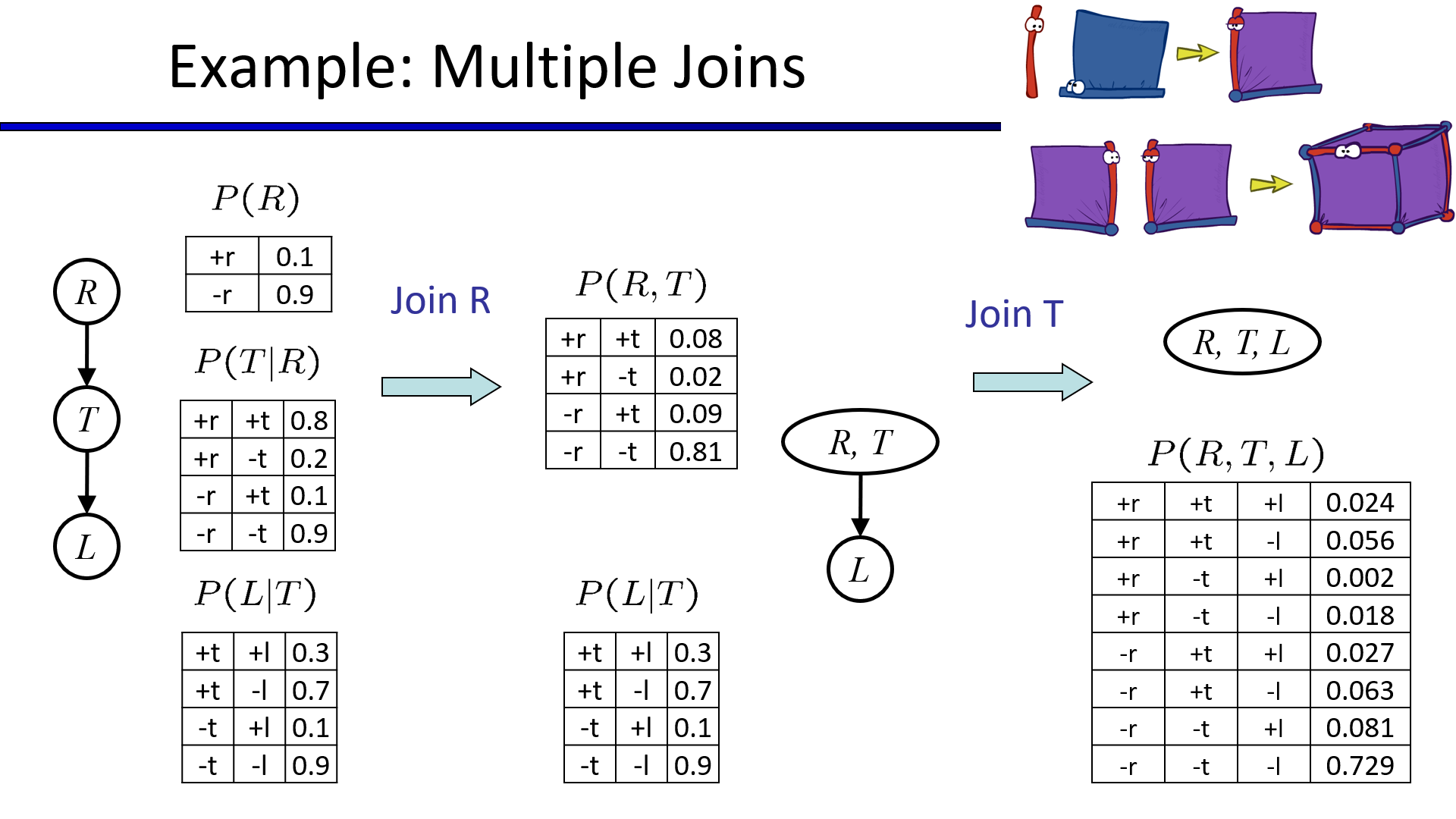
1. 枚举法(Enumeration)
将目标节点、证据节点和隐藏节点全部加入CPT表,得到一张枚举出所有情况的巨大CPT表。
预测时,直接去CPT表中找结果即可。
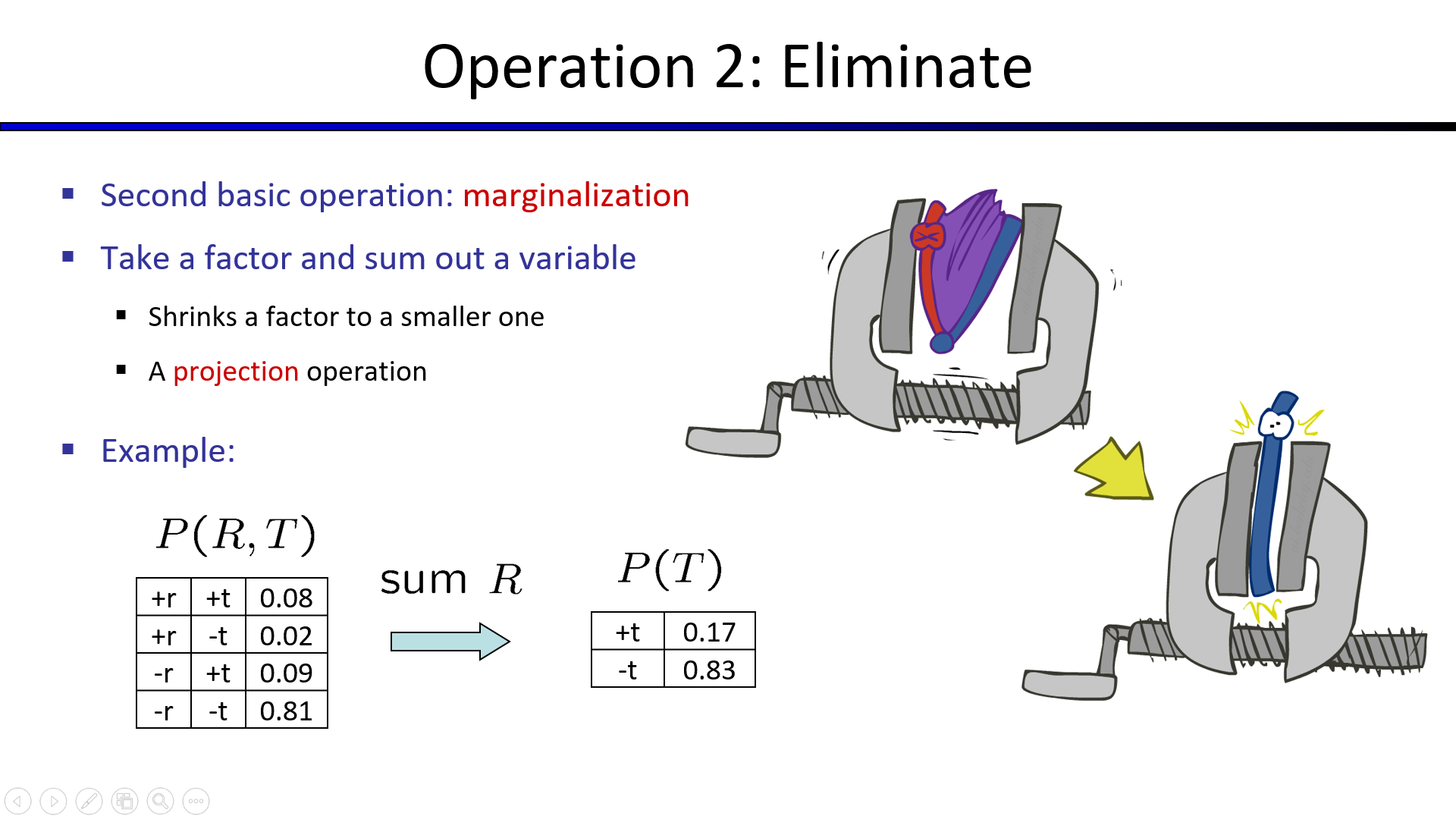
2. 消元法(Eliminate)
把所有的事件加入CPT后再进行变量消除,无异于枚举
尽早合并、消除变量才是正确的消元法
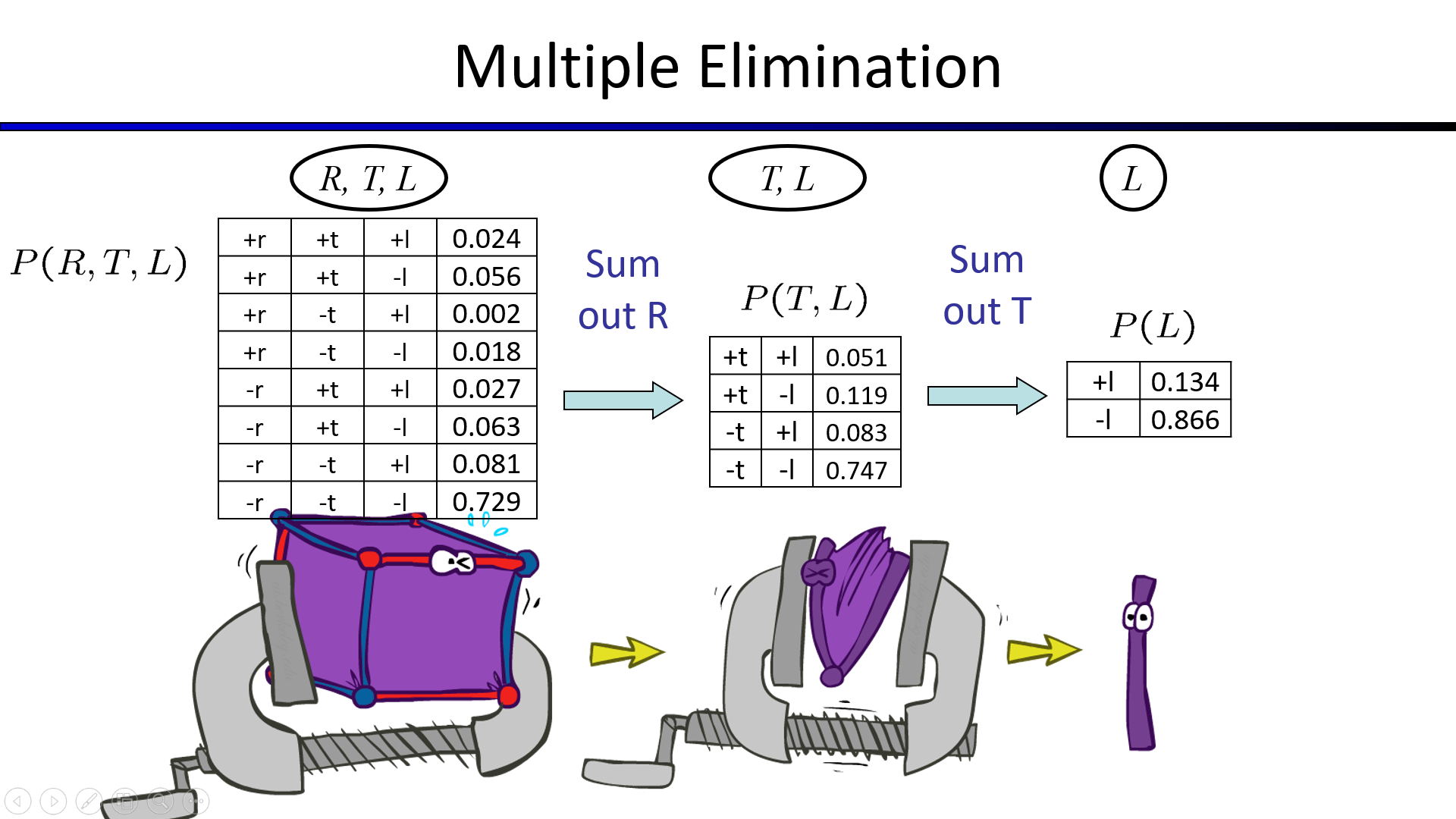
正确的消元法演示如下图右一
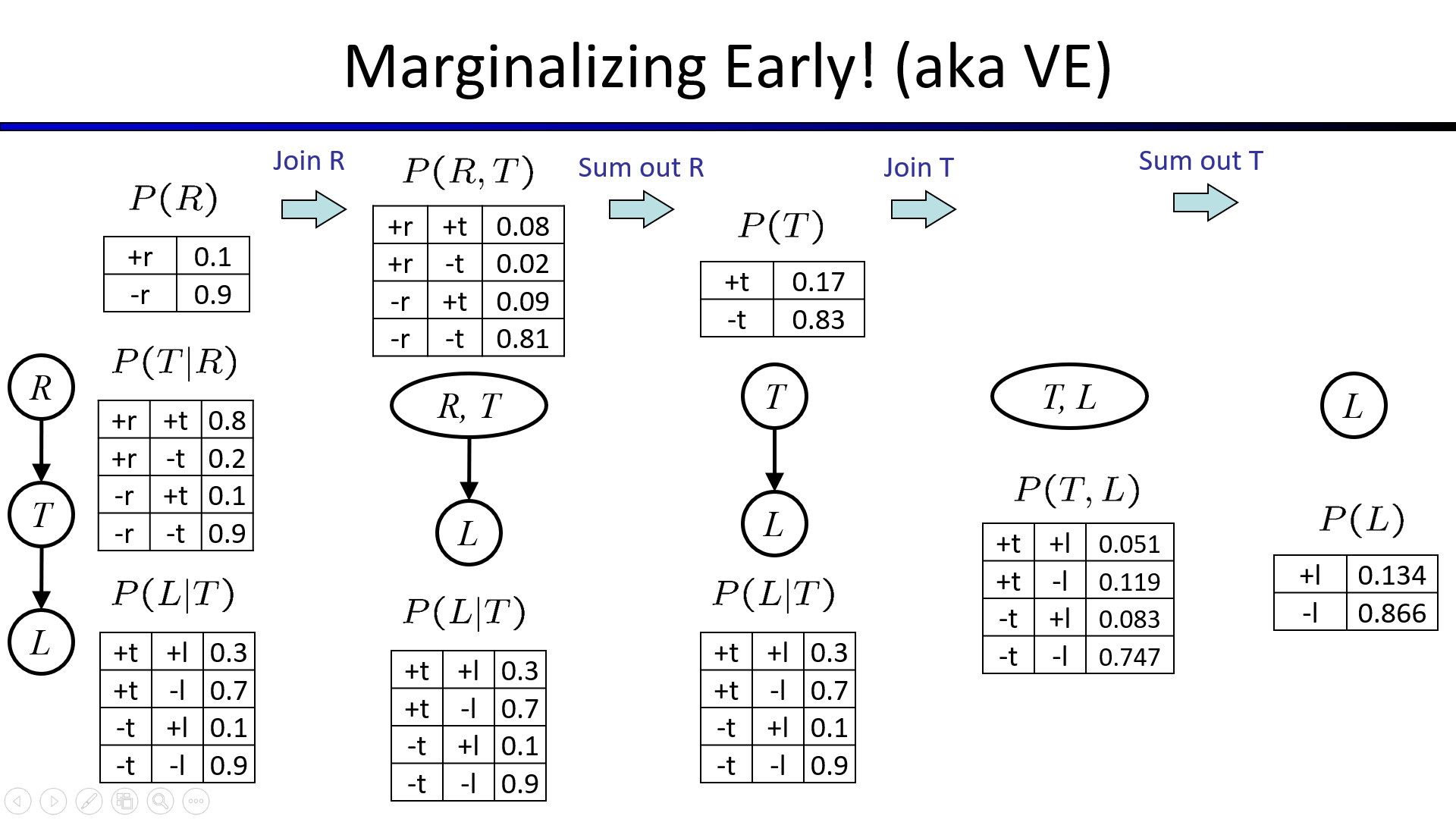
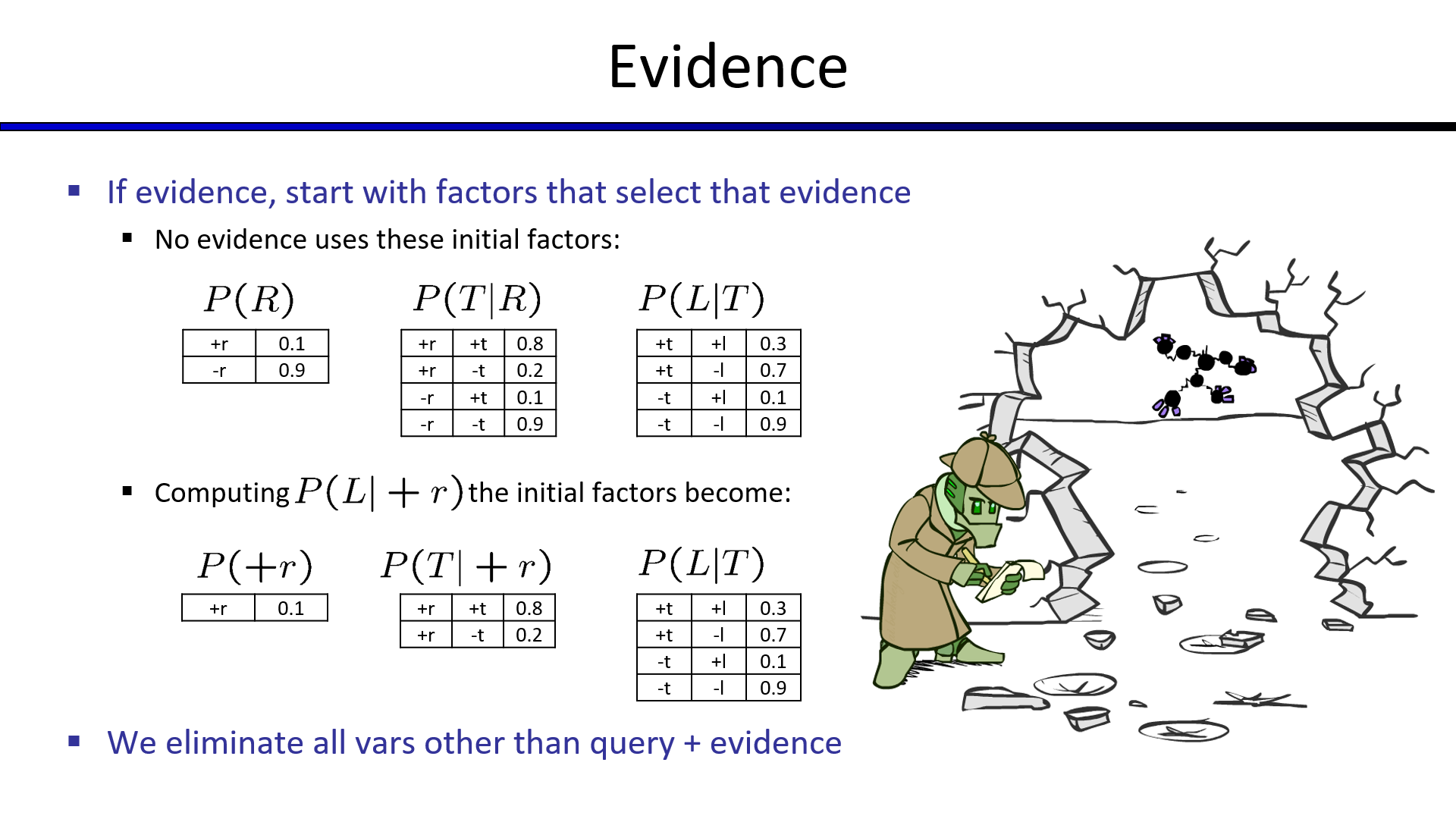
消元法使用过程演示(当起始元素是证据节点时,只需要考虑该变量的一种已知取值即可)
消元法的使用步骤总结
消元法使用举例
贝叶斯网络中的采样方法
- 贝叶斯网络中的采样方法(优先、拒绝、似然权重采样、吉布斯采样)
之所以需要使用采样求近似解,是因为当CPT网络非常大时,求精确解的代价太高了
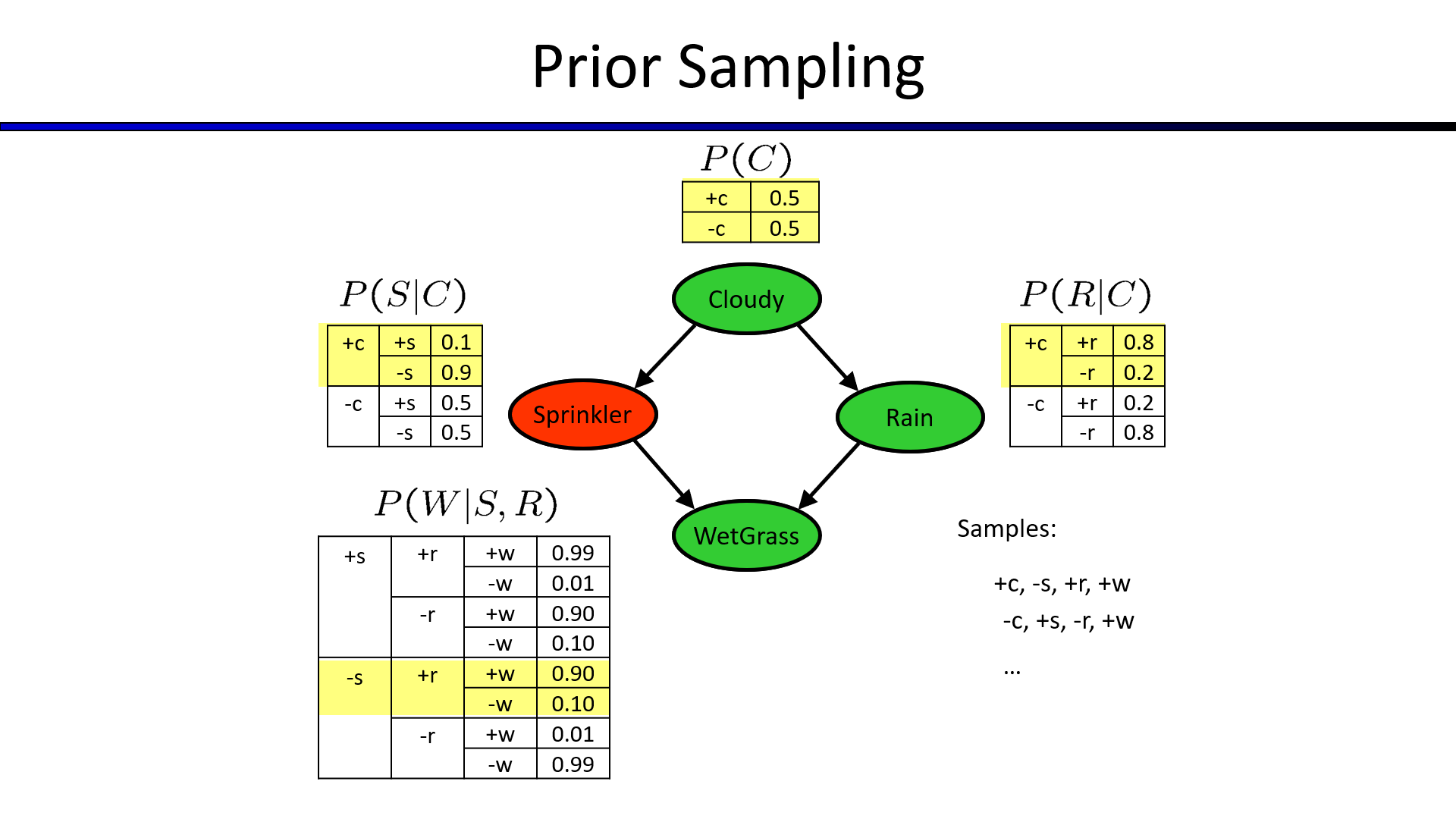
1. Prior Sampling(先验抽样)
从起始节点随机一个$value(True/False)$,之后逐步随机选择$CPT$中合理的值,直到得出目标值,根据目标值出现$True/False$的统计次数,求出平均概率。
2. Rejection Sampling(拒绝抽样)
对于不符合预期的采样结果,选择拒绝采样
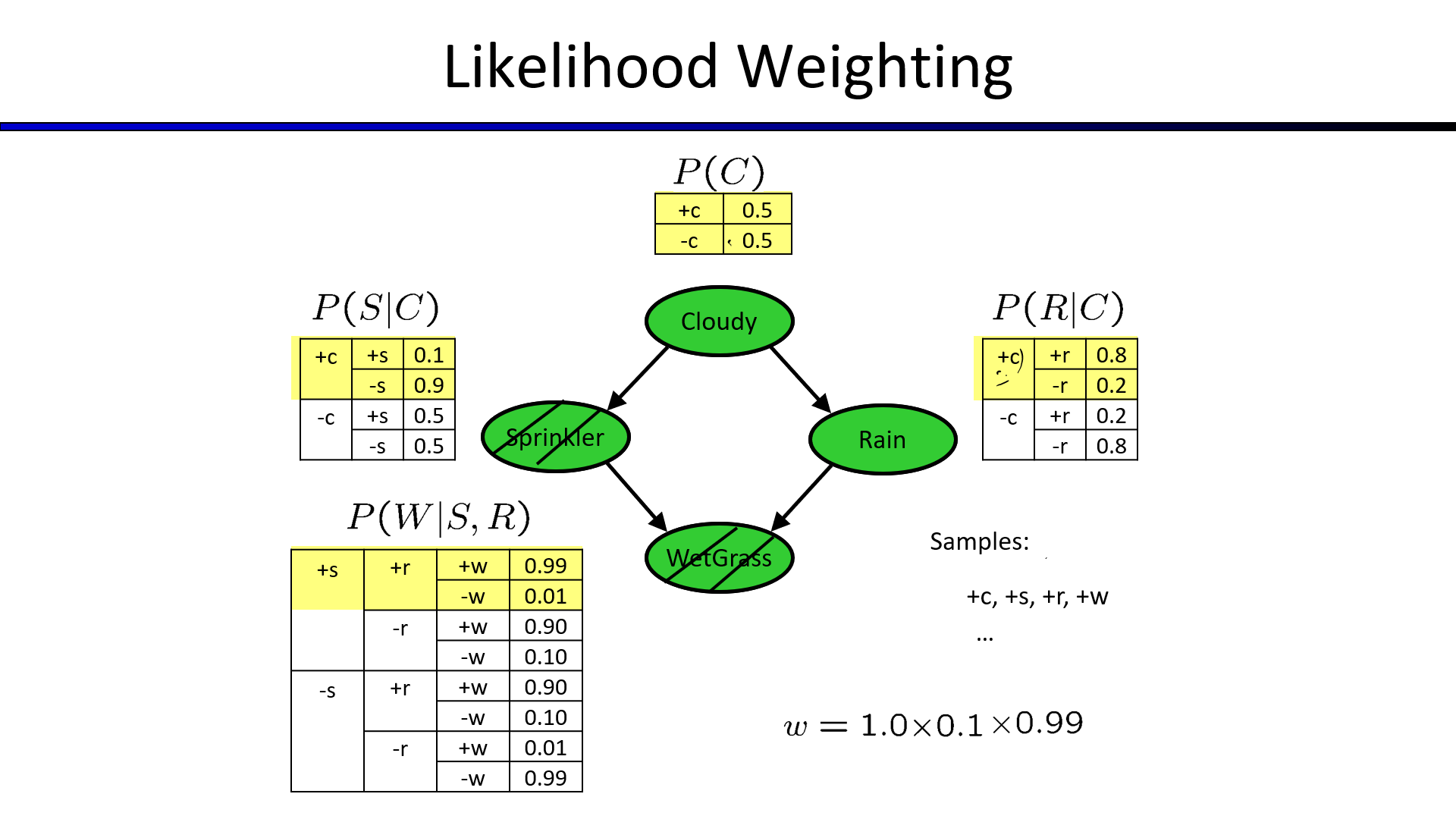
3. Likelihood Weighting(似然加权)
如果某个证据节点的出现概率很小,就会导致大量的拒绝采样
解决方法:固定该证据样本,随机选择其余的样本
固定选择证据节点$S$和$W$,为+,其余的进行随机选择,得到的目标概率如下
上述近似采样的伪代码如下
1 | IN: evidence instantiation |
似然加权虽好,但是上层的抽样结果会影响到下层的选择,但是下层的选择影响不到上层的选择,最顶端C可能抽取不到正确的选择。
(因为该方法是确定上层后向下随机选取)
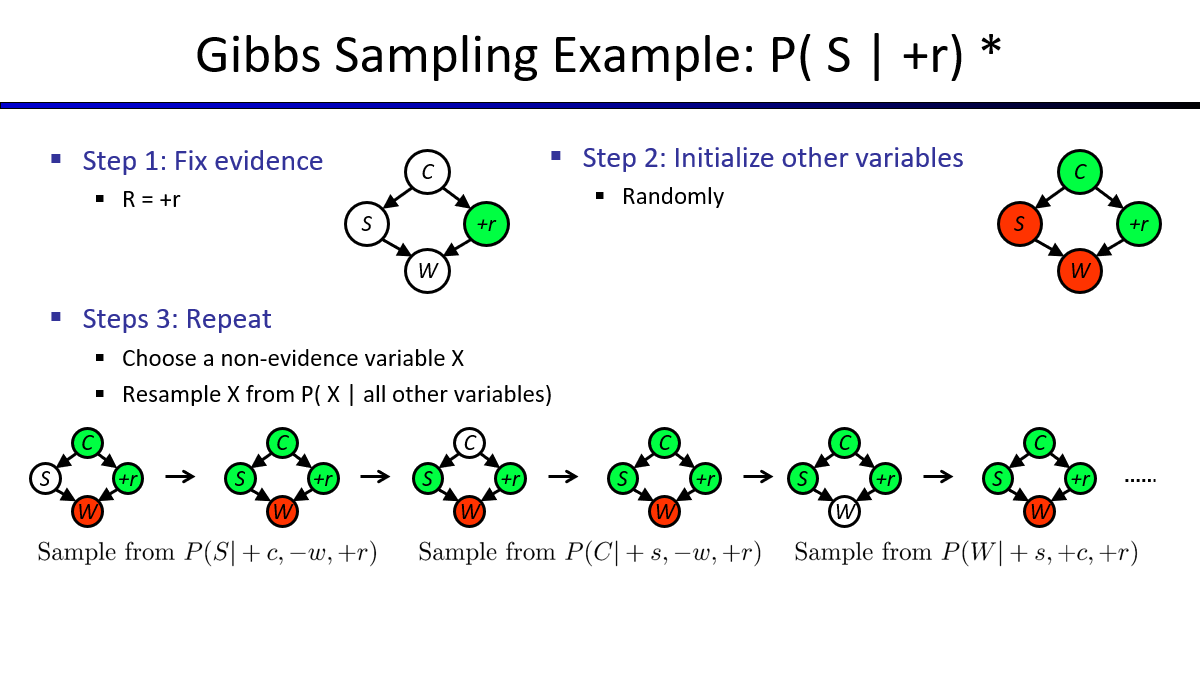
于是,我们需要吉布斯采样来解决这个问题。